پuƒsƒ^ƒSƒ‰ƒX‚ج’è—پv‚ج•تڈط–¾ڈW
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@
No.1
: Euclid 2001.03.15
ڈط–¾‚حپuƒ†پ[ƒNƒٹƒbƒhŒ´ک_پv‘و‚Pٹھ’è—‚S‚V‹y‚ر’è—‚S‚W‚ًژQڈئ
‚±‚جڈط–¾‚ھˆê”ش—¬•z‚µ‚ؤ‚¢‚éپAƒIپ[ƒ\ƒhƒbƒNƒX‚ب‚à‚ج‚إ•تٹi‚ ‚آ‚©‚¢‚إ‚·پB
No.2 :
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl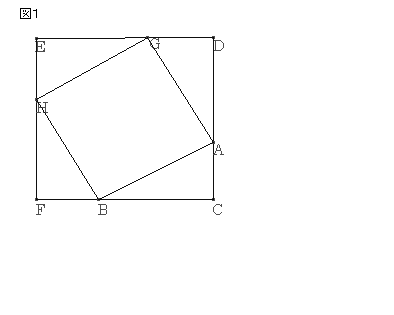
‰؛‚جگ}‚P‚حپA’¼ٹpژOٹpŒ`‚`‚a‚b‚ج‚S”{‚ئ‚ƒ²‚ئ‚إˆê‚آ‚جگ³•ûŒ`‚ًچى‚ء‚ؤ‚¢‚éپB‚»‚ê‚ًگ}‚Q‚ج‚و‚¤‚ةپA’¼ٹpژOٹpŒ`‚ً“®‚©‚·‚ئپA’¼ٹpژOٹpŒ`ژl‚آ‚ئ‚¨‚و‚ر‚إ“¯‚¶گ³•ûŒ`‚ة‚ب‚éپB‚»‚ê‚ن‚¦‚ئ‚ئ‚ح“™‚µ‚‚ب‚éپB
‚±‚ê‚ً‘مگ”“I‚ةچl‚¦‚é‚ئپA
‘ه‚«‚بگ³•ûŒ`‚جˆê•س‚حپA‚إ‚ ‚éپB’¼ٹpژOٹpŒ`‚ج–تگد‚ح‚إ‚ ‚éپB‚و‚ء‚ؤگ}‚P‚ة‚¨‚¢‚ؤ
پ@‚ƒ²پ{‚Q‚پ‚‚پپپi‚پپ{‚‚پj²
‚±‚جژ®‚ًگ®—‚·‚é‚ئپA‰؛‚ج‚و‚¤‚ة‚ب‚éپB
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.3پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
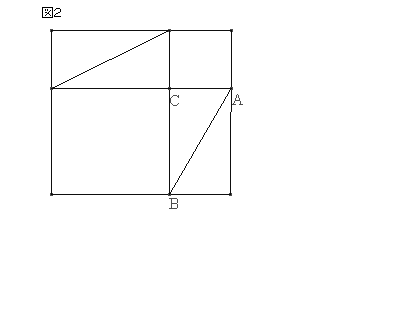
گ}‚P‚ج‘ه‚«‚بگ³•ûŒ`‚ح‰E‚ج‚و‚¤‚ة‘g‚ف‚©‚¦‚é‚ئپAگ}‚Q‚ج‚و‚¤‚ب“ٌ‚آ‚جگ³•ûŒ`‚¨‚و‚ر‚جکa‚ئ‚ب‚éپB
‚±‚ê‚ً‘مگ”“I‚ةچl‚¦‚é‚ئپAگ}‚P‚إ
پع‚b‚`‚aپپ‚e‚a‚cپAپع‚b‚a‚`پپپع‚e‚c‚aپA‚`‚aپپ‚a‚c
‚و‚ء‚ؤپA“ٌ•س‚ئ‚»‚جٹش‚جٹp‚ھپA‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚b‚`‚aپك‡™‚e‚a‚c
“¯—l‚ة‚·‚é‚ئ
ژl‚آ‚ج’¼ٹpژOٹpŒ`‚حچ‡“¯‚إ‚ ‚éپB
‚ن‚¦‚ة
پ@پ@‚ƒ²پپ‚Q‚پ‚‚پ{پi‚‚پ|‚پپj²
گ}‚P‚ًˆع“®‚µ‚ؤڈo—ˆ‚½گ}‚Q‚ًچl‚¦‚é‚ئ
پ@پ@‚پ²پ{‚‚²
‚و‚ء‚ؤ
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.‚SپF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
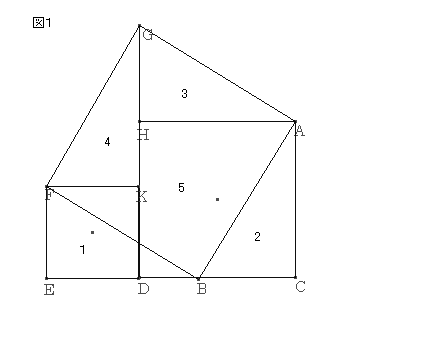
گ}‚P‚إ
‚a‚bپپ‚e‚dپپ‚پپA‚`‚bپپ‚‚پA‚`‚aپپ‚ƒ‚ئ‚µپAگ}‚P‚ج‚و‚¤‚ة‚P‚©‚ç‚T‚ً’è‚ك‚é‚ئ
‚Pپ{‚Qپ{‚Tپپپ ‚e‚d‚c‚jپ{پ ‚g‚c‚b‚`پپپ@‚پ²پ{‚‚²
‡™‚e‚d‚a‚ً‡™‚e‚j‚f‚جˆت’u‚ةپA‡™‚`‚a‚b‚ً‡™‚`‚f‚g‚جˆت’u‚ة“®‚©‚·‚ئ
‚Rپ{‚Sپ{‚Tپپپ ‚f‚e‚a‚`پپپ@‚ƒ²
‚و‚ء‚ؤ
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.5پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
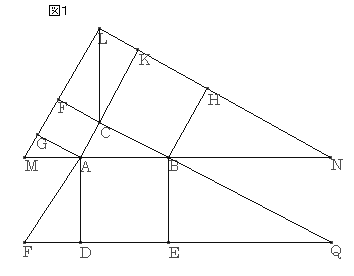
’¼ٹpژOٹpŒ`‚`‚a‚b‚¨‚و‚رپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًچى‚èپAگ³•ûŒ`‚ج•س‚ً‰„’·‚µ‚ؤپAگ}‚P‚ًچى‚éپB
‚`‚bپپ‚b‚eپC‚b‚aپپ‚e‚kپAپع‚`‚b‚aپپپع‚b‚e‚k
‚و‚ء‚ؤپA“ٌ•س‚ئ‚»‚جٹش‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
‡™‚`‚aCپك‡™‚b‚k‚e
پ@پˆ‚`‚aپپ‚k‚b
‡™‚k‚e‚b‚ًپA‚k‚lڈم‚ًٹٹ‚点پA‡™‚f‚l‚`‚ة‚‚ء‚آ‚¯‚é‚ئپAˆê‚آ‚جژOٹpŒ`‚ھ‚إ‚«
پ@‚k‚bپپ‚`‚cپAپع‚b‚k‚lپپپع‚c‚`‚oپAپع‚k‚b‚lپپپع‚`‚c‚o
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚k‚b‚lپك‡™‚`‚c‚o
پ@پˆ‡™‚k‚e‚bپ{‡™‚f‚l‚`پپ‡™‚`‚o‚cپEپEپEپEپE‡@
“¯—l‚ة‚·‚é‚ئ
پ@پ@‡™‚k‚b‚jپ{‡™‚g‚a‚mپپ‡™‚a‚d‚pپEپEپEپEپE‡A
‡@ ‚و‚è
‚k‚eپ{‚f‚lپپ‚`‚oپA‚e‚fپپ‚b‚`‚إ‚ ‚邽‚كپA‚k‚lپپ‚b‚o
‡A ‚à“¯—l‚ة‚·‚é‚ئ
‚k‚mپپ‚b‚pپC
‚ـ‚½پAپع‚l‚k‚mپپپع‚o‚b‚p‚إ‚ ‚邽‚ك
“ٌ•س‚ئ‚»‚جٹش‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚k‚l‚mپك‡™‚b‚o‚p
‚±‚ج‡™‚k‚l‚m‚ئ‡™‚b‚o‚p‚©‚ç‡@‡A‚ج“™‚µ‚¢•”•ھ‚ًˆّ‚«‹ژ‚èپA‹¤’ت•”•ھ‚إ‚ ‚釙‚`‚a‚b‚ًˆّ‚«‹ژ‚é‚ئ
پ ‚a‚g‚j‚bپ{پ ‚b‚e‚f‚`پپپ ‚`‚c‚d‚a
‚·‚ب‚ي‚؟پA
پ@پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.6پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًگ}‚P‚ج‚و‚¤‚ةچى‚éپB‚پ²‚ج’†گS‚n‚ً’ت‚ء‚ؤپA‚`‚a‚ة•½چs‚ب’¼گü‚j‚kپA‚»‚ê‚ةگ‚’¼‚ب’¼گü‚l‚m‚إ‚پ²‚ًژl‚آ‚ةگط‚éپB
‚ـ‚½پA‚a‚dپC‚c‚dپC‚`‚cپC‚`‚aڈم‚ة‚»‚ꂼ‚êپA‚a‚oپپ‚n‚mپC‚o‚dپپ‚l‚nپC‚d‚pپپ‚j‚nپC‚c‚pپپ‚n‚kپC‚c‚qپپ‚l‚nپC‚`‚qپپ‚m‚nپC‚`‚rپپ‚n‚kپC‚a‚rپپ‚j‚n‚ئ‚ب‚é‚و‚¤‚ب‚oپC‚pپC‚qپC‚r‚ً‚ئ‚èپA‚±‚ê‚ç‚جژl“_‚ً’ت‚èپA‚a‚b‚ ‚é‚¢‚ح‚`‚b‚ة•½چs‚ة‚o‚vپC‚p‚sپC‚q‚tپC‚r‚u‚ًˆّ‚پB‚»‚µ‚ؤپA‚P‚©‚ç‚T‚ًگ}‚P‚ج‚و‚¤‚ة’è‚ك‚éپB
‚o‚vپC‚p‚sپC‚q‚tپC‚r‚u‚ھ‚a‚b‚ ‚é‚¢‚ح‚`‚b‚ة•½چs‚إ‚ ‚邽‚ك
ƒj—וس‚ئژlٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚كپAژl•سŒ`‚QپC‚RپC‚SپC‚T‚حچ‡“¯‚إ‚ ‚éپB
پ@‚s‚vپپ‚o‚vپ|‚o‚sپپ‚b‚mپ|‚f‚lپپ‚b‚mپ|‚w‚mپپ‚b‚wپپ‚b‚`
پ@‚v‚uپپ‚r‚uپ|‚r‚vپپ‚k‚aپ|‚j‚bپپ‚j‚`پ|‚j‚bپپ‚b‚`
‚و‚ء‚ؤپAژl•سŒ`‚v‚u‚t‚s‚حپAگ³•ûŒ`‚ئ‚ب‚èپA–تگد‚ح‚ئ‚ب‚è‚P‚حچ‡“¯‚إ‚ ‚éپB
پˆپ ‚`‚i‚g‚jپ{پ ‚f‚b‚a‚eپپپ ‚`‚c‚d‚a
‚·‚ب‚ي‚؟پA
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.7پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًگ}‚P‚ج‚و‚¤‚ةچى‚éپB‚ـ‚½‚c‚`‚ً‰„’·‚µپA‚b‚g‚ئ‚جŒً“_‚ً‚tپA‚a‚`‚ة•½چs‚ة‚e‚l‚ًˆّ‚«‚l‚©‚çگ‚’¼‚ة‚l‚m‚ًˆّ‚پB‚d‚©‚ç‚a‚b‚ة•½چs‚ة‚d‚o‚ًˆّ‚«پA‚e‚a‚ج‰„’·‚ً‚o‚d‚ئ‚p‚إŒً‚ي‚点پA‚b‚`‚ة•½چs‚ة‚c‚s‚ًˆّ‚پB
ژl•سŒ`‚l‚`‚a‚e‚حپA•½چsژl•سŒ`‚إ‚ ‚邽‚ك
پ@‚`‚aپپ‚l‚e
پ@‚`‚aپپ‚d‚aپCپع‚b‚a‚`پپپع‚p‚a‚dپAپع‚b‚`‚aپپپع‚p‚d‚a
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚`‚a‚bپك‡™‚d‚a‚p
پ@پˆ‚a‚pپپ‚a‚bپپ‚e‚a
ژl•سŒ`‚l‚e‚a‚m‚ً‚e‚p‚ة‰ˆ‚ء‚ؤ‚·‚ׂ点پA‚l‚e‚ً‚`‚a‚ةˆê’v‚³‚¹‚é‚ئپA
ƒj—וس‚ئژlٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
ژl•سŒ`‚l‚e‚a‚mپپژl•سŒ`‚`‚o‚p‚aپEپEپEپEپEپE‡@
پ@‚l‚eپپ‚c‚dپAپع‚f‚l‚eپپپع‚s‚c‚dپAپع‚f‚l‚eپپپع‚s‚d‚c
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚l‚f‚eپك‡™‚c‚s‚dپ@پ@پ@پ@پ@پEپEپEپEپEپE‡A
پ ‚t‚o‚d‚a‚ح•½چsژl•سŒ`‚ج‚½‚ك
‚t‚oپپ‚a‚dپپ‚`‚c‚و‚è
‚t‚`پپ‚o‚cپCپع‚b‚t‚`پپپع‚s‚o‚cپCپع‚b‚`‚tپپپع‚s‚c‚o
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ“™‚µ‚¢‚½‚ك
پ@‡™‚t‚`‚bپپ‡™‚o‚c‚sپ@پ@پ@پ@پ@پEپEپEپEپEپEپE‡B
ژں‚ة‚d‚aڈم‚ة‚`‚t‚ة“™‚µ‚‚d‚q‚ً‚ئ‚èپA‚a‚b‚ة•½چs‚ة‚q‚r‚ًˆّ‚‚ئپA‘خ‚·‚éٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ ‚g‚j‚`‚tپكپ ‚r‚p‚d‚qپ@پ@پ@پ@پEپEپEپEپEپEپE‡C
‚ـ‚½پA‚t‚oپپ‚a‚d‚و‚è
پ@‚`‚oپپ‚a‚q
‚`‚oپپ‚l‚m‚إ‚ ‚é‚©‚ç
‚l‚mپپ‚a‚q
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚l‚b‚mپك‡™‚a‚r‚qپ@پ@پ@پ@پ@پ@پEپEپEپEپEپEپE‡D
‡@ ‚©‚ç‡D‚ً‚·‚ׂؤ‰ء‚¦‚é‚ئ
پ ‚g‚j‚`‚bپ{پ ‚f‚b‚a‚eپپپ ‚`‚c‚d‚a
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.8پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
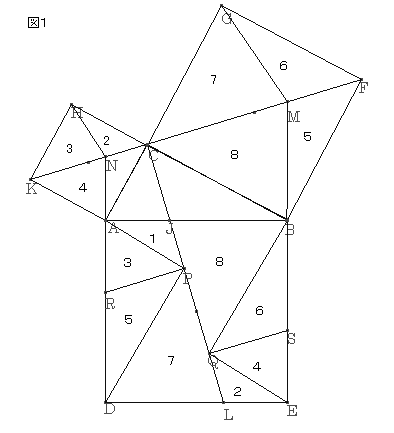
’¼ٹpژOٹpŒ`‚`‚a‚b‚ً‚آ‚‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًگ}‚P‚ج‚و‚¤‚ةچى‚éپB‚jپC‚b‚ًŒ‹‚رپA‚b‚ئ‚e‚ًŒ‹‚ش‚ئپA‚j‚b‚ئ‚b‚e‚حپAˆê’¼گü‚ئ‚ب‚éپB‚c‚`‚ج‰„’·‚ئ‚j‚b‚ئ‚جŒً“_‚ً‚m‚ئ‚µپA‚g‚ئŒ‹‚شپB‚d‚a‚ج‰„’·‚ئ‚b‚e‚ئ‚جŒً“_‚ً‚l‚ئ‚µپA‚f‚ئŒ‹‚شپB‚c‚و‚è‚`‚b‚ة•½چs‚ةˆّ‚¢‚½’¼گü‚c‚o‚ئ‚j‚`‚ج‰„’·‚ئ‚جŒً“_‚ً‚o‚ئ‚·‚éپB‚»‚µ‚ؤپA‚o‚ئ‚`‚ًŒ‹‚شپB‚d‚و‚è‚a‚b‚ةˆّ‚¢‚½’¼گü‚d‚p‚ئ‚e‚a‚ج‰„’·‚ئ‚جŒً“_‚ً‚p‚ئ‚µپA‚p‚ئ‚d‚ًŒ‹‚شپB‚ـ‚½پAگ}‚P‚ج‚و‚¤‚ة‚P‚©‚ç‚W‚ً’è‚ك‚éپB
پ@پع‚b‚`‚aپپپع‚o‚`‚cپCپع‚b‚a‚`پپپع‚o‚c‚`پC‚`‚aپپ‚`‚c
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚o‚`‚cپك‡™‚b‚`‚aپ@پ@پ@پ@پ@پ@پEپEپEپEپEپEپE‡@پ@پ@پ@پ@پ@پ@
ڈ]‚ء‚ؤپA‚bپC‚o‚ًŒ‹‚ش‚ئپA‡™‚b‚j‚o‚ح’¼ٹpژOٹpŒ`‚ئ‚ب‚è
پ@پع‚`‚b‚oپپپ@‚S‚T°
“¯—l‚ة‚·‚é‚ئ
‡™‚b‚p‚e‚حپA’¼ٹpژOٹpŒ`‚ئ‚ب‚è
پ@پع‚a‚b‚pپپپ@‚S‚Tº
‚و‚ء‚ؤپA‚b‚o‚ئ‚b‚p‚حˆê’v‚·‚éپB
پع‚m‚`‚bپپپع‚i‚`‚oپAپع‚m‚b‚`پپپع‚i‚o‚`پC‚`‚bپپ‚`‚o
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚`‚m‚bپك‡™‚`‚o‚iپ@پ@پ@پ@پ@پ@
‚ـ‚½پA‚o‚©‚ç‚j‚e‚ة•½چs‚ة‚o‚q‚ًˆّ‚‚ئ
پ@‚j‚`پپ‚`‚cپCپع‚m‚`‚jپپپع‚q‚`‚oپAپع‚m‚j‚`پپپع‚q‚o‚`
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚m‚j‚`پك‡™‚q‚`‚o
‡™‚j‚g‚mپك‡™‚m‚j‚`‚و‚è
پ@‡™‚j‚g‚mپك‡™‚q‚`‚o
‡@ ‚و‚è
‚o‚cپپ‚e‚aپAپع‚q‚c‚oپپپع‚l‚a‚eپAپع‚q‚o‚cپپپع‚l‚e‚a
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚e‚l‚aپك‡™‚o‚q‚cپ@پ@پ@پ@پ@پ@پEپEپEپEپEپEپE‡A
‡A ‚و‚è
پع‚o‚c‚kپپپع‚b‚a‚lپCپع‚k‚o‚cپپپع‚l‚b‚aپA‚o‚cپپ‚a‚b
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚b‚l‚aپك‡™‚o‚c‚k
‡™‚b‚f‚lپك‡™‚b‚l‚a‚إ‚ ‚é‚©‚ç
پ@‡™‚b‚f‚mپك‡™‚o‚c‚k
گ}‚P‚ج‚PپC‚RپC‚TپA‚V‚ً‰ء‚¦‚é‚ئ
پ@‡™‚`‚m‚bپ{‡™‚j‚g‚mپ{‡™‚e‚l‚aپ{‡™‚b‚f‚lپپژl•سŒ`‚`‚c‚k‚i
“¯—l‚ة‚·‚é‚ئ
گ}‚P‚ج‚QپC‚SپC‚UپC‚W‚ً‰ء‚¦‚é‚ئ
پ@‡™‚b‚m‚gپ{‡™‚m‚j‚`پ{‡™‚f‚l‚eپ{‡™‚l‚b‚aپپژl•سŒ`‚i‚k‚d‚a
‚±‚ج“ٌ‚آ‚ً‰ء‚¦‚é‚ئ
پ ‚g‚j‚`‚bپ{پ ‚a‚e‚f‚bپپپ ‚`‚c‚d‚a
‚و‚ء‚ؤ
پ@پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپBپ@پ@پ@پ@
‚m‚ڈ.9پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
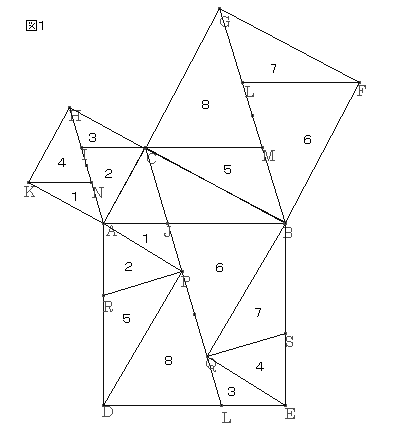
ڈم‚ج–â‘è‚ئ‚ئ“¯—l‚ة‚oپC‚pپC‚qپC‚r‚ًچى‚éپB‚»‚µ‚ؤپA‚`‚a‚ة•½چs‚إ‚b‚ً’ت‚é‚h‚lپC‚j‚mپC‚k‚e‚ًچى‚éپBگ}‚P‚ج‚و‚¤‚ة‚P‚©‚ç‚W‚ً’è‚ك‚éپB
ژl•سŒ`‚j‚m‚`‚i‚حپA•½چsژl•سŒ`‚إ‚ ‚邽‚ك
پ@‚j‚mپپ‚`‚iپCپع‚m‚j‚`پپپع‚i‚`‚oپCپع‚m‚`‚jپپپع‚i‚o‚`
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚m‚j‚`پك‡™‚i‚`‚o
پ@‚`‚bپپ‚`‚oپAپع‚b‚`‚hپپپع‚`‚o‚qپپپ@‚S‚TºپAپع‚h‚b‚`پپپع‚q‚`‚c
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚b‚h‚`پك‡™‚`‚q‚o
‚b‚aپپ‚c‚o
پع‚l‚b‚aپپپع‚q‚c‚oپiپع‚q‚c‚oپپپع‚`‚c‚oپپپع‚d‚a‚pپپپع‚`‚a‚bپپپع‚l‚b‚aپj
پ@پع‚l‚a‚bپپپع‚q‚o‚cپiپع‚q‚o‚cپپپ@‚S‚Tºپj
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚l‚b‚aپك‡™‚q‚c‚o
پ@‚f‚bپپ‚o‚cپCپع‚f‚b‚lپپپع‚o‚c‚kپCپع‚l‚f‚bپپپع‚k‚o‚cپپپ@‚S‚Tº
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚f‚b‚lپك‡™‚o‚c‚k
گ}‚P‚ج‚PپC‚QپC‚TپC‚W‚ً‰ء‚¦‚é‚ئ
‡™‚j‚m‚`پ{‡™‚b‚`‚hپ{‡™‚l‚b‚aپ{‡™‚f‚b‚lپپژl•سŒ`‚`‚c‚k‚i
“¯—l‚ة‚µ‚ؤ
گ}‚P‚ج‚RپC‚SپC‚UپC‚V‚ً‰ء‚¦‚é‚ئ
‡™‚g‚h‚bپ{‡™‚g‚j‚mپ{‡™‚a‚e‚kپ{‡™‚f‚k‚eپپژl•سŒ`‚i‚k‚d‚a
‚±‚ج“ٌ‚آ‚ً‰ء‚¦‚é‚ئ
پ ‚g‚j‚`‚bپ{پ ‚a‚e‚f‚bپپپ ‚`‚c‚d‚a
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.10پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
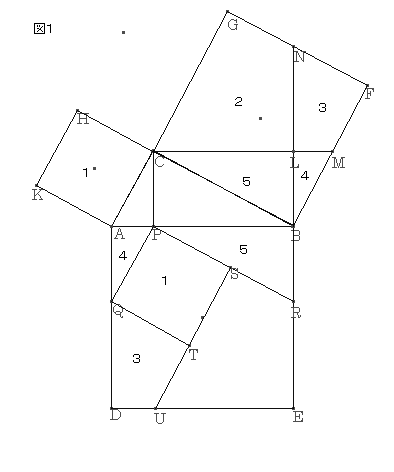
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًگ}‚P‚ج‚و‚¤‚ةچى‚éپB‚b‚و‚è‚`‚a‚ة•½چs‚ة‚b‚l‚ًˆّ‚«پA‚d‚a‚ً‰„’·‚µ‚ؤ‚a‚m‚ًچى‚éپB‚b‚©‚ç‚`‚a‚ةگ‚گü‚b‚o‚ً‰؛‚낵پA‚»‚ج‘«‚o‚©‚ç‚b‚`‚ة•½چs‚ة‚o‚pپA‚b‚a‚ة•½چs‚ة‚o‚q‚ًˆّ‚پB‚ـ‚½پA‚o‚qڈم‚ة‚`‚b‚ة“™‚µ‚‚o‚r‚ًژو‚èپA‚r‚و‚è‚o‚p‚ة•½چs‚ة‚r‚t‚ًˆّ‚«پA‚ـ‚½‚p‚و‚è‚o‚q‚ة•½چs‚ة‚p‚s‚ًˆّ‚پB
‚o‚pپپ‚b‚`پپ‚l‚aپAپع‚`‚p‚oپپپع‚k‚a‚lپCپع‚`‚o‚pپپپع‚k‚l‚a
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚k‚a‚lپك‡™‚`‚p‚o
پ@‚b‚aپپ‚o‚qپAپع‚k‚b‚aپپپع‚a‚o‚qپCپع‚k‚a‚bپپپع‚a‚q‚o
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚b‚a‚kپك‡™‚o‚q‚a
پ@‚g‚jپپ‚o‚p‚إژlٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ پ@‚g‚j‚`‚bپكپ ‚o‚p‚s‚r
‡™‚e‚m‚aپك‡™‚b‚`‚a‚و‚è
‚p‚sپپ‚`‚bپپ‚e‚m
‚p‚cپپ‚`‚cپ|‚`‚pپپ‚m‚aپ|‚k‚aپپ‚m‚k
‚©‚آپAژlٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@ژl•سŒ`‚m‚k‚l‚eپكژl•سŒ`‚p‚c‚t‚s
‚q‚dپپ‚a‚dپ|‚a‚qپپ‚m‚aپ|‚k‚aپپ‚m‚k
پ@‚t‚dپپ‚c‚dپ|‚c‚tپپ‚b‚lپ|‚k‚lپپ‚b‚k
‚©‚آپAژlٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@ژl•سŒ`‚f‚b‚k‚mپكژl•سŒ`‚r‚t‚d‚q
گ}‚P‚ج‚PپA‚QپC‚RپC‚SپC‚T‚ً‰ء‚¦‚é‚ئ
پ ‚g‚j‚`‚bپ{پ ‚a‚e‚f‚bپپپ ‚`‚a‚d‚c
‚·‚ب‚ي‚؟
پ@پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.11پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
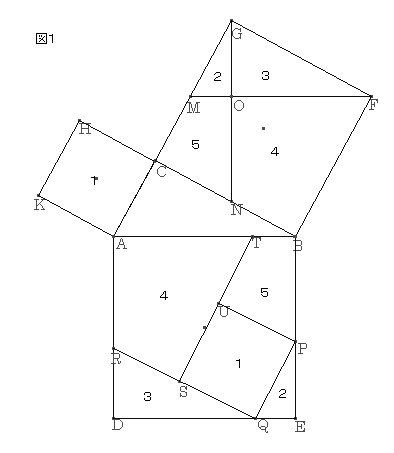
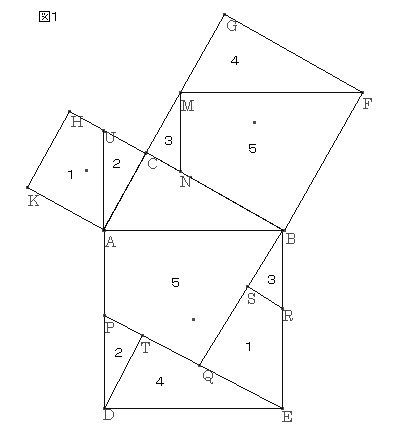
گ}‚P‚ج‚و‚¤‚ة’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًچى‚éپB‚e‚©‚ç‚`‚a‚ة•½چs‚ة‚e‚l‚ًˆّ‚«پC‚f‚©‚ç‚`‚a‚ةگ‚’¼‚ة‰؛‚낵پA‚a‚b‚ئ‚جŒً“_‚ً‚mپC‚e‚l‚ئ‚جŒً“_‚ً‚n‚ئ‚·‚éپB‚a‚oپپ‚n‚mپC‚o‚dپپ‚f‚n‚ئ‚ب‚é‚و‚¤‚ب“_‚p‚ً‚ئ‚éپB‚`‚cڈم‚ة‚`‚qپپ‚n‚mپC‚q‚cپپ‚f‚n‚ئ‚ب‚é‚و‚¤‚ب“_‚q‚ً‚ئ‚èپA‚`‚aڈم‚ة‚`‚sپپ‚n‚eپC‚s‚aپپ‚l‚n‚ئ‚ب‚é‚و‚¤‚ب“_‚s‚ً‚ئ‚éپB‚s‚©‚ç‚`‚b‚ة•½چs‚ة‚s‚r‚ًˆّ‚پB‚ـ‚½پAگ}‚P‚ج‚و‚¤‚ة‚P‚©‚ç‚T‚ً’è‚ك‚éپB
پع‚f‚l‚nپپپع‚o‚p‚dپCپع‚f‚n‚lپپپع‚o‚d‚pپC‚l‚nپپ‚p‚d
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚f‚l‚nپك‡™‚o‚p‚dپ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپEپEپEپE‡@
پ@پع‚f‚n‚eپپپع‚q‚c‚pپCپع‚f‚e‚nپپپع‚q‚p‚cپC‚n‚eپپ‚c‚p
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚f‚n‚eپك‡™‚q‚c‚pپ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپEپEپE‡A
ژl•سŒ`‚n‚m‚a‚e‚ئ‚`‚q‚r‚s‚ح
پع‚`‚q‚rپپپع‚q‚c‚pپ{پع‚q‚p‚cپپپع‚p‚o‚dپ{پ@‚X‚Oºپ@پپپع‚l‚f‚nپ{پ@‚X‚O°پ@پپپع‚n‚m‚a
‚و‚ء‚ؤپA“ٌ—וس‚ئژlٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚كچ‡“¯‚ئ‚ب‚éپBپEپEپEپE‡B
ژl•سŒ`‚b‚l‚n‚m‚ئ‚t‚s‚a‚o‚ح
“ٌ—וس‚ئژlٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚كچ‡“¯‚ئ‚ب‚éپBپEپEپEپEپEپE‡C
‡@پA‡™‚f‚l‚eپك‡™‚b‚`‚a‚و‚è
پ@‚o‚pپپ‚f‚lپپ‚b‚`
‡CپA‡™‚f‚b‚mپك‡™‚a‚b‚`پi‚f‚bپپ‚e‚fپCپع‚f‚b‚mپپپع‚e‚f‚lپCپع‚b‚f‚mپپپع‚f‚e‚lپCپˆ‡™‚f‚b‚mپك‡™‚f‚l‚eپj‚و‚è
پ@‚o‚tپپ‚m‚bپپ‚b‚`
‚و‚ء‚ؤپAژl•سŒ`‚o‚p‚r‚t‚حپA“ٌ—וس‚ھ“™‚µ‚ژlٹp‚ھ“™‚µ‚¢‚½‚كگ³•ûŒ`‚ئ‚ب‚éپB
گ}‚P‚ج‚P‚©‚ç‚T‚ً‰ء‚¦‚é‚ئپAپ ‚`‚a‚d‚c‚ة“ü‚éپB
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.1‚QپF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
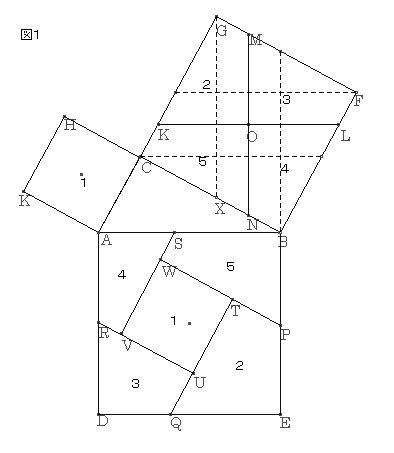
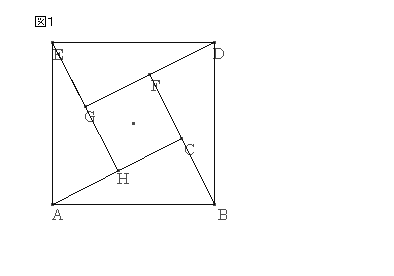
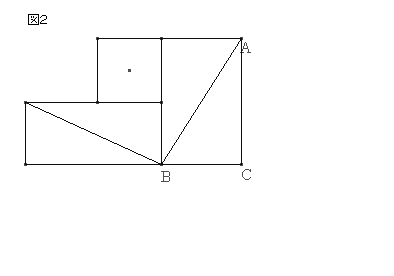
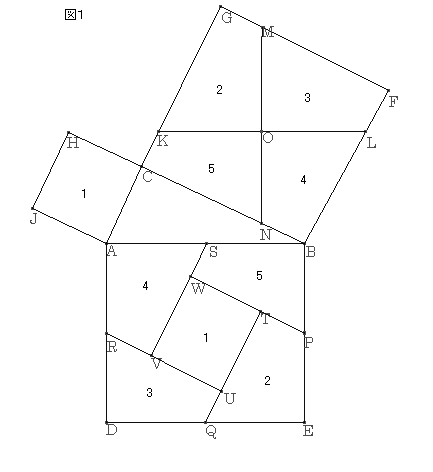
گ³ژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًچى‚éپBگ}‚P‚ج“_گü‚إˆح‚ـ‚ꂽ•”•ھ‚ة’†گS‚n‚ًژ‚؟پA‚`‚a‚ة•½چs‚¨‚و‚رگ‚’¼‚ب‚Q’¼گü‚j‚kپC‚l‚m‚ًˆّ‚پB‚ـ‚½پA‚a‚dپC‚d‚cپC‚c‚`پC‚`‚aڈم‚ة‚»‚ꂼ‚ê‚a‚oپپ‚n‚mپC‚o‚dپپ‚l‚nپC‚d‚pپپ‚j‚nپC‚c‚pپپ‚n‚kپC‚c‚qپپ‚l‚nپC‚`‚qپپ‚n‚mپC‚`‚rپپ‚n‚kپC‚a‚rپپ‚j‚n‚ئ‚ب‚é‚و‚¤‚ب‚oپC‚pپC‚qپC‚r‚ً‚ئ‚éپBژں‚ةپA‚±‚ê‚ç‚ج‚S“_‚ً’ت‚èپA‚a‚b‚ ‚é‚¢‚حپA‚`‚b‚ة•½چs‚ة‚o‚vپC‚p‚sپC‚q‚tپC‚r‚u‚ًˆّ‚پBگ}‚P‚ج‚و‚¤‚ة‚P‚©‚ç‚T‚ً’è‚ك‚éپB
ژl•سŒ`‚QپC‚RپC‚SپC‚T‚حپA“ٌ—וس‚ئ‘خ‰‚·‚éژlٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚كچ‡“¯‚ئ‚ب‚éپB
پ@‚s‚vپپ‚o‚vپ|‚o‚sپپ‚b‚mپ|‚f‚lپپ‚b‚mپ|‚m‚wپپ‚b‚wپپ‚b‚`
پ@‚u‚vپپ‚r‚uپ|‚r‚vپپ‚a‚kپ|‚j‚bپپ‚j‚`پ|‚j‚bپپ‚b‚`
‚و‚ء‚ؤپAژl•سŒ`‚v‚u‚t‚s‚حپAˆê•س‚ج’·‚³‚ھ‚‚‚جگ³•ûŒ`‚ئ‚ب‚èپAپ ‚`‚b‚g‚i‚ئچ‡“¯‚ئ‚ب‚éپB
‚آ‚ـ‚èپAگ}‚P‚ج‚P‚©‚ç‚T‚ً‚·‚ׂؤ‰ء‚¦‚é‚ئپAپ ‚`‚a‚d‚c‚ئˆê’v‚·‚éپB
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.13پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
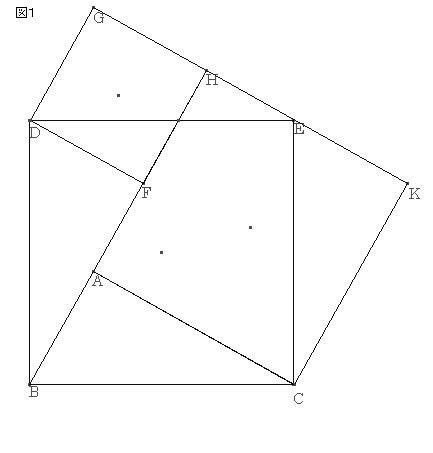
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚`‚bپC‚a‚bڈم‚ةگ³•ûŒ`‚ًگ}‚P‚ج‚و‚¤‚ةچى‚éپB‚c‚©‚ç‚a‚g‚ةگ‚گü‚ًˆّ‚«‚e‚ئ‚µپA‚c‚eڈم‚ةگ³•ûŒ`‚ًچى‚éپB
گ³•ûŒ`‚a‚b‚d‚c‚ھپAگ³•ûŒ`‚c‚e‚g‚d‚ئگ³•ûŒ`‚`‚b‚j‚g‚جکa‚ئ“™‚µ‚¢ژ–‚ًژ¦‚·پB
پ@‚c‚dپپ‚d‚bپCپع‚d‚b‚jپپپ|پع‚j‚d‚bپپپع‚f‚d‚cپAپع‚b‚d‚jپپپع‚d‚c‚f
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚f‚c‚dپك‡™‚j‚d‚b
پ@‚c‚dپپ‚c‚aپCپع‚e‚c‚aپپپ@‚X‚O°پ@پ|پع‚d‚c‚eپپپع‚f‚c‚dپAپع‚c‚a‚eپپپع‚c‚d‚f
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚f‚c‚dپكپع‚e‚c‚a
پ@‚c‚aپپ‚a‚bپAپع‚e‚c‚aپپ‚X‚O°پ|پع‚e‚a‚cپپپع‚`‚a‚bپAپع‚e‚a‚cپپپع‚`‚b‚a
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚e‚c‚aپك‡™‚`‚a‚b
‚ن‚¦‚ة
پ@پ@‡™‚f‚c‚dپك‡™‚j‚d‚bپك‡™‚e‚c‚aپك‡™‚`‚a‚b
کZ•سŒ`‚c‚e‚`‚b‚d‚c‚حپA‹¤’ت•”•ھ‚إ‚ ‚é‚ج‚إپAگ³•ûŒ`‚a‚b‚d‚c‚حپAگ³•ûŒ`‚c‚e‚g‚d‚ئگ³•ûŒ`‚`‚b‚j‚g‚جکa‚ئ“™‚µ‚¢پB
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.14پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
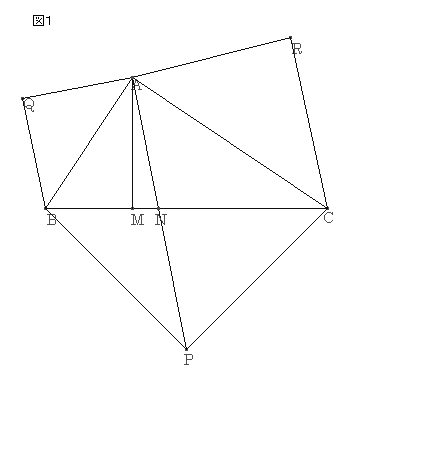
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ة’¼ٹp“ٌ“™•سژOٹpŒ`‚ًگ}‚P‚ج‚و‚¤‚ةچى‚éپB‚`‚©‚ç‚a‚b‚ةگ‚گü‚ً‰؛‚낵پA‚a‚b‚ئ‚جŒً“_‚ً‚l‚ئ‚·‚éپB
ژl“_‚`‚a‚o‚b‚حپA“¯ˆê‰~ژüڈم‚ة‚ ‚é‚ئچl‚¦‚ç‚ê‚邽‚ك
‚a‚oپپ‚b‚o‚و‚è
پ@پع‚a‚`‚oپپپع‚o‚`‚bپپپ@‚S‚T°پ@پپپع‚p‚a‚`
پ@پˆپ@‚`‚o//‚p‚a
‚و‚ء‚ؤ
پ@پ@‡™‚`‚p‚aپپ‡™‚o‚p‚aپ@پ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپEپE‡@
ژl“_‚`‚p‚a‚g‚حپA“¯ˆê‰~ژüڈم‚ة‚ ‚é‚ئچl‚¦‚ç‚ê‚邽‚ك
پ@پع‚p‚l‚aپپپع‚p‚g‚`پپپ@‚S‚Tºپ@پپپع‚o‚a‚l
پ@پˆپ@‚p‚l//‚a‚o
‚و‚ء‚ؤ
پ@پ@‡™‚o‚a‚pپپ‡™‚o‚l‚aپ@پ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپEپE‡A
‡@‡A‚و‚è
پ@پ@‡™‚`‚p‚aپپ‡™‚o‚l‚a
“¯—l‚ة‚µ‚ؤ
پ@‚a‚oپپ‚b‚o‚و‚è
پ@پع‚a‚`‚oپپپع‚o‚`‚bپپپپپع‚q‚b‚`
پ@پ@پˆپ@‚`‚o//‚q‚b
‚و‚ء‚ؤ
پ@پ@‡™‚`‚q‚bپپ‡™‚o‚q‚bپ@پ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپEپE‡B
ژl“_‚`‚q‚b‚g‚حپA“¯ˆê‰~ژüڈم‚ة‚ ‚é‚ئچl‚¦‚ç‚ê‚邽‚ك
پ@پع‚`‚l‚qپپپع‚q‚l‚bپپپپپع‚o‚b‚a
پ@پ@پˆپ@‚q‚l//‚b‚o
‚و‚ء‚ؤ
پ@پ@‡™‚q‚o‚bپپ‡™‚l‚o‚bپ@پ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپEپE‡C
‡B‡C‚و‚è
پ@پ@‡™‚`‚q‚bپپ‡™‚l‚o‚b
‚ن‚¦‚ة
پ@پ@‡™‚`‚p‚aپ{‡™‚`‚q‚bپپ‡™‚o‚a‚b
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.15پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
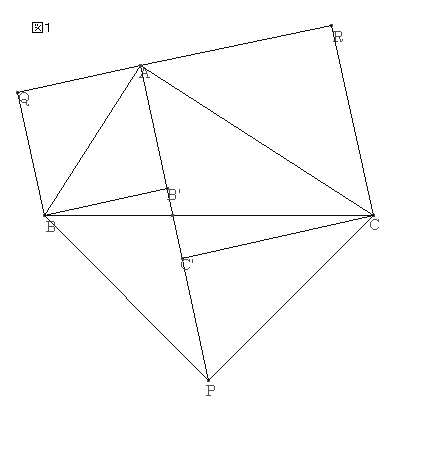
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ة’¼ٹp“ٌ“™•سژOٹpŒ`‚ًگ}‚P‚ج‚و‚¤‚ةچى‚éپB‚aپC‚b‚©‚ç‚`‚o‚ضگ‚گü‚ً‰؛‚낵‚`‚o‚ئ‚جŒً“_‚ًB`پAC`‚ئ‚·‚éپB
‘O–â‘è‚و‚è
پ@‚`‚o//‚a‚p//‚b‚q
پ@‚o‚aپپ‚b‚oپCپع‚a‚o‚a`پپپع‚c‚b‚b`پAپع‚o‚a‚a`پپپع‚b‚o‚b`
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚o‚a‚a`پك‡™‚o‚b‚b`
پ@‚`‚oپپ‚`‚a`پ{‚a`‚oپپ‚`‚pپ{‚b‚b`پپ‚`‚pپ{‚`‚qپپ‚p‚q
پ@‚Q‚`‚a‚o‚bپپ‚`‚oپ~پi‚a‚a`پ{‚b‚b`پjپپپ@‚`‚o²
پ@‚Q‚a‚p‚q‚bپپ‚p‚qپ~پi‚a‚pپ{‚b‚qپjپپپ@‚`‚o²
پ@پ@پˆپ@ژl•سŒ`‚`‚a‚o‚bپپژl•سŒ`‚a‚p‚q‚b
‚و‚ء‚ؤ
پ@‡™‚o‚a‚bپپ‡™‚p‚`‚aپ{‡™‚q‚b‚`
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.16پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ة’¼ٹp“ٌ“™•سژOٹpŒ`‚ًگ}‚P‚ج‚و‚¤‚ةچى‚éپB
پ@‚a‚bپپ‚o‚bپC‚b‚qپپ‚b‚`پAپع‚a‚b‚qپپپع‚o‚b‚`
‚و‚ء‚ؤپA“ٌ•س‚ئ‚»‚جٹش‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚a‚b‚qپك‡™‚`‚b‚oپ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپEپE‡@
‚ن‚¦‚ة
پ@‚a‚qپپ‚o‚`پA‚a‚pپپ‚a‚`پCپع‚p‚a‚qپپپع‚`‚a‚o
‚و‚ء‚ؤپA“ٌ•س‚ئ‚»‚جٹش‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚a‚p‚qپك‡™‚`‚a‚oپ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپEپE‡A
‡@‡A‚و‚è
پ@ژl•سŒ`‚a‚p‚q‚bپپژl•سŒ`‚`‚a‚o‚b
‚±‚جژ®‚ج—¼•س‚©‚燙‚`‚a‚b‚ًژو‚èڈœ‚‚ئ
پ@‡™‚o‚a‚bپپ‡™‚p‚`‚aپ{‡™‚q‚b‚`
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.17پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًگ}‚P‚ج‚و‚¤‚ةچى‚éپB‚`‚©‚ç‚a‚bپC‚c‚d‚ةگ‚گü‚ً‰؛‚낵پA‚»‚ꂼ‚ê‚جŒً“_‚ً‚lپC‚k‚ئ‚·‚éپB‚`‚k‚ً‰„’·‚µ‚ؤ‚e‚f‚ج‰„’·‚ئ‚جŒً“_‚ً‚m‚ئ‚·‚éپB
پ@‚`‚fپپ‚a‚`پCپع‚m‚`‚fپپپع‚b‚a‚`پCپع‚m‚f‚`پپپع‚b‚`‚a
‚و‚ء‚ؤپA“ٌ•س‚ئ‚»‚جٹش‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚`‚f‚mپك‡™‚`‚a‚b
‚ن‚¦‚ة
پ@‚`‚mپپ‚a‚bپپ‚k‚l
‚c‚a‚ج‰„’·‚ئ‚e‚m‚ئ‚جŒً“_‚ً‚o‚ئ‚·‚é‚ئ
’ê•س‚ئچ‚‚³‚ھ“™‚µ‚¢‚½‚ك
پ@’·•ûŒ`‚a‚c‚k‚lپپ•½چsژl•سŒ`‚o‚a‚`‚mپ@پ@پ@پ@پEپEپEپEپE‡@
‚`‚a‚ھ‹¤’ت‚إپAچ‚‚³‚ھ“™‚µ‚¢‚½‚ك
پ@پ ‚`‚a‚e‚fپپ•½چsژl•سŒ`‚o‚a‚`‚mپ@پ@پ@پ@پ@پ@پEپEپEپEپE‡A
‡@‡A‚و‚è
پ@’·•ûŒ`‚a‚c‚l‚kپپپ ‚`‚a‚e‚f
“¯—l‚ة‚·‚é‚ئ
پ@’·•ûŒ`‚l‚k‚d‚bپپپ ‚`‚b‚j‚g
‚و‚ء‚ؤ
پ ‚`‚a‚e‚fپ{پ ‚`‚b‚j‚gپپ’·•ûŒ`‚a‚c‚l‚kپ{’·•ûŒ`‚l‚k‚d‚bپپپ ‚a‚c‚d‚b
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.18پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚b‚و‚è‚`‚a‚ضگ‚گü‚b‚c‚ً‰؛‚ë‚·پB
‘خ‰‚·‚éژOٹp‚ھپA‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚`‚a‚bپن‡™‚`‚c‚b
پ@پˆ‚`‚aپF‚`‚bپپ‚`‚bپF‚`‚c
پ@‚`‚b²پ@پپ‚`‚aپE‚`‚c
پ@پ@پ@پ@‚‚²پ@پپ‚ƒپE‚`‚cپ@پ@پ@پ@پ@پ@پEپEپEپEپEپEپE‡@
‘خ‰‚·‚éژOٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚`‚a‚bپن‡™‚c‚a‚b
پ@پˆ‚`‚aپF‚a‚bپپ‚a‚bپF‚c‚a
پ@پ@پ@‚a‚b²پ@پپ‚`‚aپE‚c‚a
پ@پ@پ@‚پ²پ@پپ‚ƒپE‚c‚aپ@پ@پ@پ@پ@پ@پEپEپEپEپEپEپEپE‡A
‡@ ‚ئ‡A‚ً‰ء‚¦‚é‚ئ
پ@‚پ²پ{‚‚²پ@پپ‚ƒپEپi‚`‚cپ{‚c‚aپjپپپ@‚ƒ²
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.19پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚b‚و‚è‚`‚a‚ضگ‚گü‚b‚c‚ً‰؛‚ë‚·پB
پi‚P‚Vپj‚و‚è
پ@‡™‚`‚a‚bپن‡™‚`‚c‚bپن‡™‚c‚a‚b
‚و‚ء‚ؤپA‘ٹژ—‚بژOٹpŒ`‚ج–تگد‚ج”ن‚حپA‘خ‰•س‚ج‚Qڈو”ن‚ة“™‚µ‚¢‚½‚ك
c ²/ ‡™‚`‚a‚bپپپ@‚‚²پ@/‡™‚`‚c‚bپپپ@‚پ²
/‡™‚c‚a‚b
پ@پ@‚ن‚¦‚ة
پ@پ@‚ƒ²پ@/‡™‚`‚a‚bپپپ@‚‚²پ{‚پ²پ@/پi‡™‚`‚c‚bپ{‡™‚c‚a‚bپj
پ@‡™‚`‚a‚bپپ‡™‚`‚c‚bپ{‡™‚c‚a‚b
‚·‚ب‚ي‚؟
پ@ ‚پ²+b²=c²
‚ئ‚ب‚éپB
‚m‚ڈ.20پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
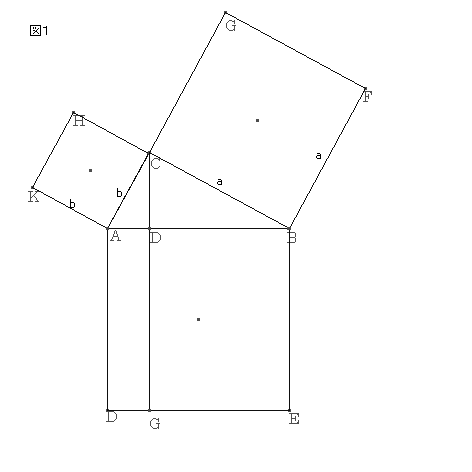
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًچى‚éپB‚b‚©‚ç‚`‚aپC‚d‚e‚ةگ‚گü‚ً‰؛‚낵پA‚`‚aپC‚d‚e‚جŒً“_‚ً‚cپC‚f‚ئ‚·‚éپB
پi‚P‚Vپj‚و‚è
پ@‡™‚`‚a‚bپن‡™‚`‚b‚c
پ@‚`‚cپF‚`‚bپپ‚`‚bپF‚`‚a
پ@پ@ b² پپ‚`‚cپE‚`‚dپ@پ@پ@پ@پ@پ@پ@پEپEپEپEپEپEپE‡@
پ@‚`‚cپF‚`‚aپپ‚`‚cپF‚`‚d
پ@‚`‚aپE‚`‚cپپ‚`‚cپE‚`‚d
‡@ ‚و‚è
b² پپ‚`‚cپE‚`‚aپپ‚`‚cپE‚`‚dپپ’·•ûŒ`‚`‚f
پ@‚`‚aپF‚a‚bپپ‚a‚bپF‚c‚a
پ@پ@ ‚پ² پپ‚`‚aپE‚c‚aپ@پ@پ@پ@پ@پ@پEپEپEپEپEپEپEپE‡A
پ@‚c‚aپF‚`‚aپپ‚c‚aپF‚a‚e
پ@‚`‚aپF‚c‚aپپ‚a‚eپF‚c‚a
‡A ‚و‚è
‚پ² پپ‚`‚aپE‚c‚aپپ‚a‚eپE‚c‚aپپ’·•ûŒ`‚a‚f
پ@‚پ²پ{‚‚²پپ’·•ûŒ`‚`‚fپ{’·•ûŒ`‚a‚f پپپ@c²
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.21پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
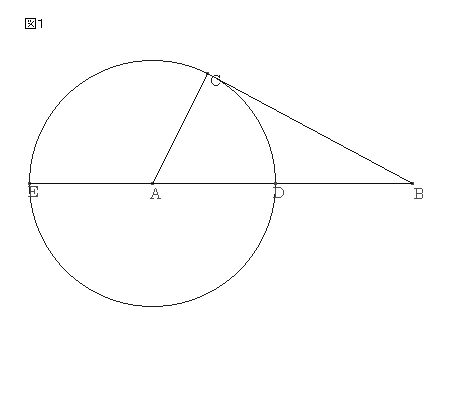
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚`‚ً’†گS‚ئ‚µ‚`‚b‚ً”¼Œa‚ئ‚·‚é‰~‚ًچى‚éپB‰~‚ئ‚`‚a‚ئ‚جŒً“_‚ً‚cپC‚`‚a‚ج‰„’·گü‚ئ‚جŒً“_‚ً‚d‚ئ‚·‚éپB‚±‚ج‰~‚حپA“_‚b‚إ‚a‚b‚ئگع‚·‚éپB
پ@‡™‚c‚a‚bپن‡™‚b‚a‚d‚و‚è
پ@‚a‚cپF‚a‚bپپ‚a‚bپF‚a‚d
پ@پ@‚a‚b²پ@پپ‚a‚cپE‚a‚d
‚a‚cپپ‚`‚aپ|‚`‚cپA‚a‚dپپ‚`‚aپ{‚`‚d‚و‚è
پ@پ@‚a‚b²پ@پپپi‚`‚aپ|‚`‚bپjپi‚`‚aپ{‚`‚bپj
پ@پ@پ@پپپ@‚`‚a²پ|‚`‚b²
پ@پ@‚`‚a²پ@پپپ@‚a‚b²پ@پ{پ@‚`‚b²
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.22پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
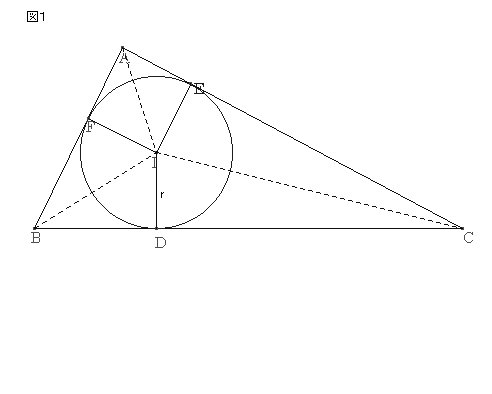
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‡™‚`‚a‚b‚ة“_‚n‚ً’†گS‚ئ‚·‚é“àگع‰~‚ًچى‚èپA‚n‚©‚ç‚`‚bپC‚`‚aپC‚a‚b‚ةگ‚گü‚ً‰؛‚낵پAگع“_‚ً‚dپC‚eپC‚c‚ئ‚·‚éپB‚±‚ج“àگع‰~‚ج”¼Œa‚ً‚’‚ئ‚·‚éپB
‚e‚hپپ‚c‚hپCپع‚a‚e‚hپپپع‚a‚c‚hپAپع‚a‚h‚eپپپع‚a‚h‚c
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚a‚h‚eپك‡™‚a‚h‚c
“¯—l‚ة‚·‚é‚ئ
پ@‡™‚b‚d‚hپك‡™‚b‚c‚h
پ@‚rپپ‚’²پ{‚QپE‚P/‚Q·a‚’پپ‚’پi‚’پ{‚پپjپپ‚“‚’پ@پ@پ@پ@پEپEپEپEپE‡@
پ@‚rپپپ@‚P/‚Q·‚‚‚ƒپ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپE‡A
پ@‚پپپپi‚ƒپ|‚’پjپ{پi‚‚پ|‚’پj
پ@پ@پپ‚‚پ{‚ƒپ|‚Q‚’
پ@‚’پپپ@‚P/‚Qپi‚‚پ{‚ƒپ|‚پپj
پ@‚rپپپ@‚P/‚Qپi‚پپ{‚‚پ{‚ƒپj
‡@‡A‚و‚è
پ@‚rپپپ@‚P/‚QپE‚‚‚ƒپپپ@‚P/‚Sپi‚پپ{‚‚پ{‚ƒپjپi‚‚پ{‚ƒپ|‚پپj
پ@پ@‚Q‚‚‚ƒپپپi‚پپ{‚‚پ{‚ƒپjپi‚‚پ{‚ƒپ|‚پپj
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.23پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
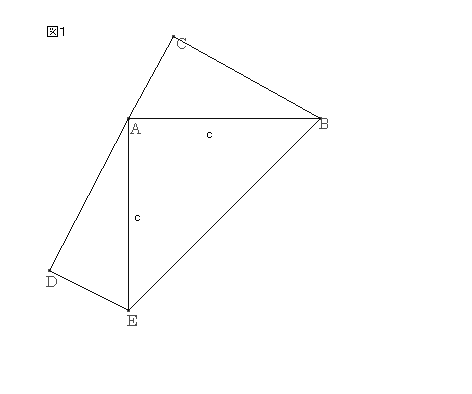
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپAگ}‚P‚ج‚و‚¤‚ة‚`‚a‚ةگ‚’¼‚ة‚`‚d‚ًˆّ‚«پA‚`‚aپپ‚`‚d‚ئ‚·‚éپBژں‚ةپA‚b‚`‚ً‰„’·‚µ‚ؤ‚`‚cپپ‚b‚a‚ئ‚ب‚é‚و‚¤‚ة‚µپA‚cپC‚d‚ًŒ‹‚شپB
‚`‚aپپ‚`‚dپC‚a‚bپپ‚`‚cپAپع‚b‚a‚`پپپع‚c‚`‚d
‚و‚ء‚ؤپA“ٌ•س‚ئ‚»‚جٹش‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚`‚c‚dپك‡™‚`‚a‚b
پ@ژl•سŒ`‚c‚d‚a‚bپپپ@‚P/‚Qپi‚پپ{‚‚پj²
‚ـ‚½پA
پ@ژl•سŒ`‚c‚d‚a‚bپپ‚Q‡™‚`‚a‚bپ{‡™‚`‚a‚d
پ@پ@پ@پ@پ@پ@پ@پ@پپ‚پ‚‚پ{‚P/‚QپE‚ƒ²
‚و‚ء‚ؤ
پ@‚P/‚Qپi‚پپ{‚‚پj²پ@پپ‚پ‚‚پ{پ@‚P/‚QپE‚ƒ²
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.24پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
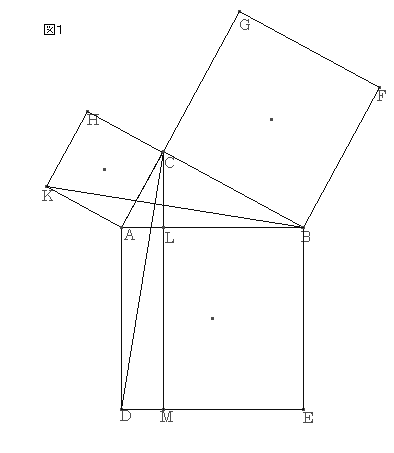
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًچى‚éپB‚b‚©‚ç‚`‚a‚ةگ‚گü‚b‚k‚l‚ًˆّ‚پB‚ـ‚½‚jپC‚a‚¨‚و‚ر‚bپA‚c‚ًŒ‹‚شپB
‡™‚b‚`‚c‚ئ’·•ûŒ`‚`‚c‚l‚k‚حپA’ê•س‚ھ‹¤’ت‚إچ‚‚³‚ھ“™‚µ‚¢‚½‚ك
پ@’·•ûŒ`‚`‚c‚l‚kپپ‚Q‡™‚b‚`‚c
پ@‚j‚`پپ‚`‚bپC‚`‚aپپ‚`‚cپCپع‚j‚`‚aپپپع‚b‚`‚c
‚و‚ء‚ؤپA“ٌ•س‚ئ‚»‚جٹش‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@‡™‚b‚`‚cپك‡™‚j‚`‚a
‡™‚j‚`‚a‚ئپ ‚j‚`‚b‚g‚حپA’ê•س‚ھ‹¤’ت‚إچ‚‚³‚ھ“™‚µ‚¢‚½‚ك
پ ‚j‚`‚b‚gپپ‚Q‡™‚j‚`‚a
‚ن‚¦‚ة
پ ‚j‚`‚b‚gپپ’·•ûŒ`‚`‚c‚l‚k
“¯—l‚ة‚·‚é‚ئ
پ ‚a‚b‚f‚eپپ’·•ûŒ`‚k‚l‚d‚a
ڈم‚ج“ٌ‚آ‚ً‰ء‚¦‚é‚ئ
پ ‚j‚`‚b‚gپ{پ ‚a‚b‚f‚eپپپ ‚`‚a‚d‚c
‚و‚ء‚ؤ
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.25پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
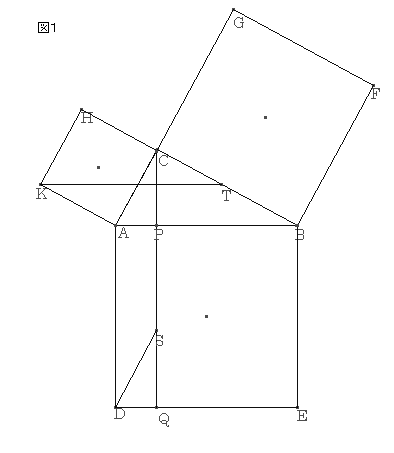
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًچى‚éپB‚b‚©‚ç‚`‚a‚ةگ‚’¼‚ة‚b‚o‚p‚ًˆّ‚پB‚ـ‚½پA‚j‚©‚ç‚`‚a‚ة•½چs‚ة‚j‚s‚ًˆّ‚«‚c‚©‚ç‚`‚b‚ة•½چs‚ة‚c‚r‚ًˆّ‚پB
’ê•س‚ھ“™‚µ‚چ‚‚³‚ھ“™‚µ‚¢‚½‚ك
پ@پ@’·•ûŒ`‚`‚c‚p‚oپپ•½چsژl•سŒ`‚`‚c‚r‚bپ@پ@پ@پ@پEپEپEپEپE‡@
پ@‚j‚`پپ‚b‚`پC‚`‚aپپ‚`‚cپCپع‚j‚`‚aپپپع‚b‚`‚c
‚و‚ء‚ؤ
پ@پ@•½چsژl•سŒ`‚`‚c‚r‚bپك•½چsژl•سŒ`‚`‚a‚s‚jپ@پ@پEپEپEپEپE‡A
’ê•س‚ھ‹¤’ت‚إچ‚‚³‚ھ“™‚µ‚¢‚½‚ك
پ@پ@•½چsژl•سŒ`‚`‚a‚s‚jپپپ ‚j‚`‚b‚gپ@پ@پ@پ@پ@پ@پEپEپEپEپE‡B
‡@‡A‡B‚و‚è
پ@پ@’·•ûŒ`‚`‚c‚p‚oپپپ ‚j‚`‚b‚g
“¯—l‚ة‚·‚é‚ئ
پ@پ@’·•ûŒ`‚o‚p‚d‚aپپپ ‚a‚e‚f‚b
پˆپ@’·•ûŒ`‚`‚c‚p‚oپ{’·•ûŒ`‚o‚p‚d‚aپپپ ‚j‚`‚b‚gپ{پ ‚a‚e‚f‚bپپپ ‚`‚a‚d‚c
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.26پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
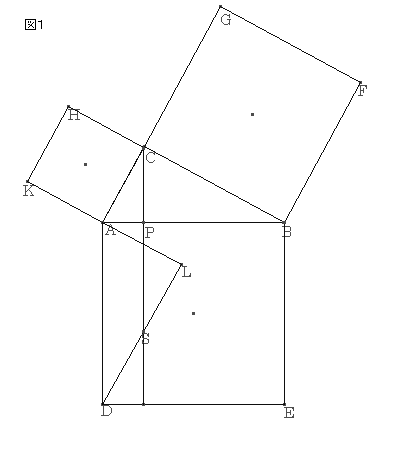
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًچى‚éپB‚b‚©‚ç‚`‚a‚ةگ‚گü‚b‚o‚p‚ًچى‚éپB‚ـ‚½‚c‚©‚ç‚`‚b‚ة•½چs‚ب‰„’·گü‚ج‚b‚p‚ئ‚جŒً“_‚ً‚rپA‚j‚`‚ئ‚ج‰„’·گü‚ئ‚جŒً“_‚ً‚k‚ئ‚·‚éپB
پ@‚`‚aپپ‚`‚cپAپع‚b‚`‚aپپپع‚k‚`‚cپAپع‚b‚a‚`پپپع‚k‚c‚`
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚`‚a‚bپك‡™‚`‚c‚k
‚ن‚¦‚ة
پ@‚`‚kپپ‚`‚bپپ‚`‚j
‚µ‚½‚ھ‚ء‚ؤپA’ê•س‚`‚b‚ھ‹¤’ت‚إچ‚‚³‚ھ“™‚µ‚¢‚©‚ç
پ@پ@•½چsژl•سŒ`‚`‚c‚r‚bپپپ ‚j‚`‚b‚g
‚m‚ڈ25‚و‚è
پ@پ@’·•ûŒ`‚`‚c‚p‚oپپ•½چsژl•سŒ`‚`‚c‚r‚b
پ@پ@’·•ûŒ`‚`‚c‚p‚oپپپ ‚j‚`‚b‚g
“¯—l‚ة‚·‚é‚ئ
پ@پ@’·•ûŒ`‚o‚p‚d‚aپپپ ‚a‚e‚f‚b
‚±‚ج“ٌ‚آ‚ً‰ء‚¦‚é‚ئ
پ ‚j‚`‚b‚gپ{پ ‚a‚e‚f‚bپپ’·•ûŒ`‚`‚c‚p‚oپ{’·•ûŒ`‚o‚p‚d‚aپپپ ‚`‚a‚d‚c
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.27پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
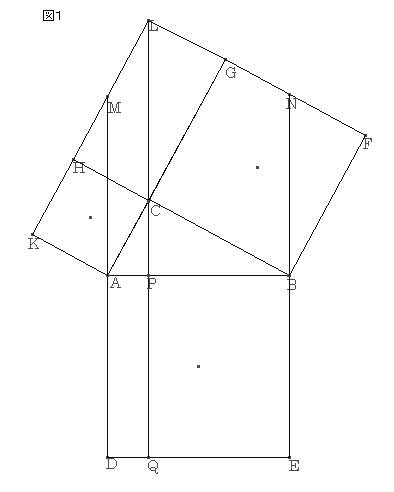
’¼ٹpژOٹpŒ`‚`‚a‚b‚ً‚آ‚‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًچى‚éپB‚b‚©‚ç‚`‚a‚ةگ‚گü‚ً‰؛‚낵پA‚`‚a‚ئ‚جŒً“_‚ً‚oپC‚c‚d‚ئ‚جŒً“_‚ً‚p‚ئ‚·‚éپB‚j‚g‚ج‰„’·‚ئ‚e‚f‚ج‰„’·‚ئ‚جŒً“_‚ً‚k‚ئ‚µپA‚kپC‚b‚ًŒ‹‚شپB‚ـ‚½پA‚c‚`‚ً‰„’·‚µ‚ؤ‚k‚j‚ئ‚جŒً“_‚ً‚l‚ئ‚·‚éپB
‚`‚bپپ‚b‚gپC‚b‚aپپ‚g‚kپCپع‚`‚b‚aپپپع‚b‚g‚k
‚و‚ء‚ؤپA“ٌ•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚`‚a‚bپك‡™‚k‚g‚b
پ@پˆ‚k‚bپپ‚`‚aپپ‚`‚c
ژl•سŒ`‚l‚`‚b‚k‚حپA•½چsژl•سŒ`‚إ‚ ‚邽‚كپA’ê•س‚ئچ‚‚³‚ھ“™‚µ‚
پ@پ@’·•ûŒ`‚`‚c‚p‚oپپ•½چsژl•سŒ`‚l‚`‚b‚kپ@پ@پ@پ@پ@پEپEپEپEپEپEپE‡@
‚ـ‚½پA•½چsژl•سŒ`‚l‚`‚b‚k‚ئپ ‚j‚`‚b‚g‚حپA’ê•س‚ئچ‚‚³‚ھ“™‚µ‚¢‚½‚ك
پ@پ@•½چsژl•سŒ`‚l‚`‚b‚kپپپ ‚j‚`‚b‚gپ@پ@پ@پ@پ@پ@پ@پEپEپEپEپEپEپE‡A
‡@‡A‚و‚è
’·•ûŒ`‚`‚c‚p‚dپپپ ‚j‚`‚b‚g
“¯—l‚ة‚·‚é‚ئ
پ@پ@’·•ûŒ`‚o‚p‚d‚aپپپ ‚a‚e‚f‚b
‚±‚ج“ٌ‚آ‚ً‰ء‚¦‚é‚ئ
پ ‚j‚`‚b‚gپ{پ ‚a‚e‚f‚bپپ’·•ûŒ`‚`‚c‚p‚dپ{’·•ûŒ`‚o‚p‚d‚aپپپ ‚`‚a‚d‚c
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.28پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
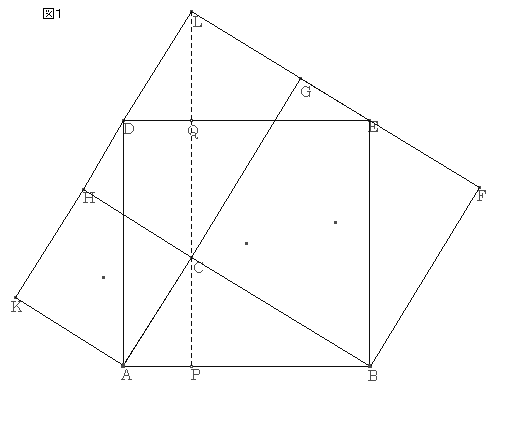
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپAگ}‚P‚ج‚و‚¤‚ة‚`‚bپC‚a‚b‚ج•سڈم‚ةگ³•ûŒ`‚ًچى‚éپB‚j‚g‚ج‰„’·‚ئ‚e‚f‚ج‰„’·‚ئ‚جŒً“_‚ً‚k‚ئ‚·‚éپB
پ@‚`‚bپپ‚`‚jپCپع‚a‚`‚bپپپع‚c‚`‚jپCپع‚`‚b‚aپپپع‚`‚j‚c
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚j‚`‚cپك‡™‚`‚a‚bپ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپE‡@
پ@‚a‚bپپ‚a‚eپCپع‚a‚b‚`پپپع‚a‚e‚dپCپع‚`‚a‚bپپپع‚d‚a‚e
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚d‚a‚eپك‡™‚`‚a‚bپ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپE‡A
‡@‡A‚و‚è
پ@‚c‚`پپ‚d‚aپپ‚`‚a
‚و‚ء‚ؤپAژl•سŒ`‚c‚`‚a‚d‚حپAگ³•ûŒ`‚ئ‚ب‚éپB
•½چsژl•سŒ`‚k‚b‚`‚c‚ئ’·•ûŒ`‚حپA’ê•س‚ئچ‚‚³‚ھ“™‚µ‚¢‚½‚ك
پ@پ@•½چsژl•سŒ`‚k‚b‚`‚cپپ’·•ûŒ`‚c‚p‚o‚`پ@پ@پ@پ@پ@پEپEپEپEپE‡B
•½چsژl•سŒ`‚k‚b‚`‚c‚ئپ ‚j‚`‚b‚g‚حپA’ê•س‚ئچ‚‚³‚ھ“™‚µ‚¢‚½‚ك
پ@پ@•½چsژl•سŒ`‚k‚b‚`‚cپپپ ‚j‚`‚b‚gپ@پ@پ@پ@پ@پ@پ@پEپEپEپEپE‡C
‡B‡C‚و‚è
پ@پ@’·•ûŒ`‚c‚`‚o‚pپپپ ‚j‚`‚b‚gپ@پ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپE‡D
“¯—l‚ة‚·‚é‚ئ
پ@پ@’·•ûŒ`‚p‚o‚a‚dپپپ ‚f‚b‚a‚eپ@پ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپE‡E
‡D‚ئ‡E‚ً‰ء‚¦‚é‚ئ
پ ‚j‚`‚b‚gپ{پ ‚f‚b‚a‚eپپ’·•ûŒ`‚c‚`‚o‚pپ{’·•ûŒ`‚p‚o‚a‚dپپپ ‚`‚a‚d‚c
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.29پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
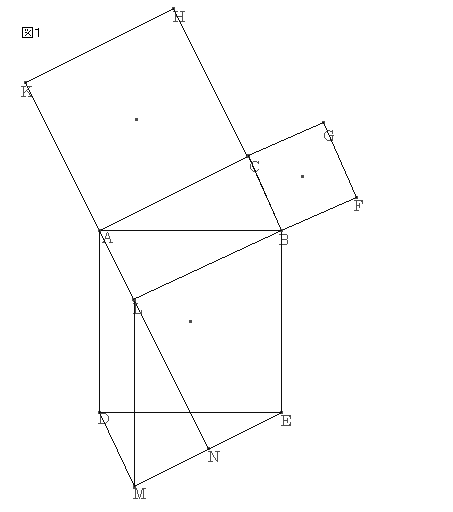
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًچى‚éپB‚j‚`‚ج‰„’·‚ئ‚e‚a‚ج‰„’·‚ئ‚جŒً“_‚ً‚k‚ئ‚µپA‚ـ‚½پA‚c‚©‚ç‚`‚k‚ة•½چs‚ة‚c‚l‚ًˆّ‚«پA‚d‚©‚ç‚a‚k‚ة•½چs‚ة‚d‚l‚ًˆّ‚«پA‚»‚جŒً“_‚ً‚l‚ئ‚·‚éپB‚j‚k‚ج‰„’·‚ئ‚d‚l‚جŒً“_‚ً‚m‚ئ‚·‚éپB
پ@‚`‚a‹¤’تپAپع‚b‚`‚aپپپع‚k‚a‚`پAپع‚b‚a‚`پپپع‚k‚`‚a
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚b‚`‚aپك‡™‚k‚a‚`پ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپEپE‡@
پ@‚`‚aپپ‚d‚cپCپع‚b‚a‚`پپپع‚l‚c‚dپAپع‚b‚`‚aپپپع‚l‚d‚c
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚b‚`‚aپپ‡™‚l‚d‚cپ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپEپE‡A
‡@‡A‚و‚è
پ@پ@‡™‚b‚`‚aپپ‡™‚k‚a‚`پپ‡™‚l‚d‚cپ@پ@پ@پ@پEپEپEپEپE‡B
‚`‚c‚l‚k‚ئ‚k‚l‚d‚a‚حپA•½چsژl•سŒ`‚ئ‚ب‚邽‚ك
پ@‚k‚lپپ‚`‚cپپ‚`‚a
پ@‚k‚lپپ‚`‚aپCپع‚b‚a‚`پپپع‚k‚l‚mپAپع‚b‚`‚aپپپع‚m‚k‚l
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚k‚l‚mپك‡™‚`‚a‚b
پ@پˆپ@‚k‚mپپ‚`‚bپپ‚`‚j
پ ‚j‚`‚b‚g‚ئ•½چsژl•سŒ`‚k‚l‚d‚a‚حپA’ê•س‚ئچ‚‚³‚ھ“™‚µ‚¢‚½‚ك
پ ‚j‚`‚b‚gپپ•½چsژl•سŒ`‚k‚l‚d‚a
“¯—l‚ة‚·‚é‚ئ
پ ‚a‚e‚f‚bپپ•½چsژl•سŒ`‚`‚c‚l‚k
‚µ‚½‚ھ‚ء‚ؤپA‡B‚و‚è
پ ‚`‚c‚d‚aپپپ ‚`‚c‚d‚aپ{‡™‚c‚l‚dپ|‡™‚`‚k‚a
پپ•½چsژl•سŒ`‚`‚c‚l‚kپ{•½چsژl•سŒ`‚k‚l‚d‚a
پپپ ‚j‚`‚b‚gپ{پ ‚b‚a‚e‚f
‚·‚ب‚ي‚؟
پ@پ@‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB
‚m‚ڈ.30پF
ƒsƒ^ƒSƒ‰ƒX‚ج’è—پ@‘ه–îگ^ˆê’کپ@ژQچl
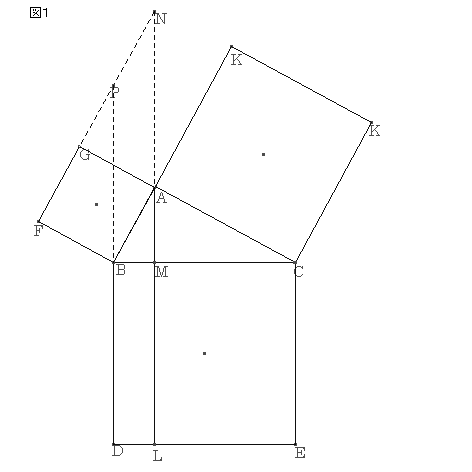
’¼ٹpژOٹpŒ`‚`‚a‚b‚ًچى‚èپA‚»‚ꂼ‚ê‚ج•سڈم‚ةگ³•ûŒ`‚ًچى‚éپB‚jپC‚b‚¨‚و‚ر‚bپC‚e‚ًŒ‹‚شپB‚b‚a‚ة•½چs‚ة‚c‚kپC‚b‚`‚ة•½چs‚ة‚d‚k‚ًˆّ‚«پAŒً“_‚k‚ئ‚b‚ئ‚ًŒ‹‚رپA‚gپC‚f‚ًŒ‹‚شپB
پ@‚`‚aپپ‚d‚cپCپع‚b‚a‚`پپپع‚k‚c‚dپAپع‚b‚`‚aپپپع‚k‚d‚c
‚و‚ء‚ؤپAˆê•س‚ئ‚»‚ج—¼’[‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚b‚`‚aپك‡™‚k‚d‚cپ@پ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپEپE‡@
پ@‚`‚bپپ‚g‚bپC‚a‚bپپ‚f‚bپCپع‚`‚b‚aپپپع‚g‚b‚f
‚و‚ء‚ؤپA“ٌ•س‚ئ‚»‚جٹش‚جٹp‚ھ‚»‚ꂼ‚ê“™‚µ‚¢‚½‚ك
پ@پ@‡™‚b‚`‚aپك‡™‚b‚g‚fپ@پ@پ@پ@پ@پ@پ@پ@پ@پEپEپEپEپEپE‡A
‡@‡A‚و‚è
پ@پ@‡™‚`‚a‚bپك‡™‚c‚k‚dپك‡™‚g‚b‚f
پ@‚j‚`پپ‚b‚`پC‚`‚aپپ‚`‚cپA‚a‚eپپ‚c‚kپAپع‚j‚`‚aپپپع‚b‚`‚cپAپع‚`‚a‚eپپپع‚`‚c‚k‚إ‚ ‚é‚©‚ç
پ@پ@ژl•سŒ`‚j‚`‚a‚eپكژl•سŒ`‚b‚`‚c‚k
“¯—l‚ة‚·‚é‚ئ
پ@پ@ژl•سŒ`‚j‚e‚f‚gپكژl•سŒ`‚b‚k‚d‚a
‚±‚ج“ٌ‚آ‚ً‰ء‚¦‚é‚ئ
پ@پ@کZ•سŒ`‚j‚`‚a‚e‚f‚gپپکZ•سŒ`‚b‚`‚c‚c‚k‚d‚a
چ¶•س‚©‚燙‚g‚b‚fپ{‡™‚`‚a‚bپپ‚Q‡™‚`‚a‚b‚©‚çˆّ‚¢‚ؤپA‰E•س‚©‚燙‚c‚k‚dپ{‡™‚`‚a‚bپپ‚Q‡™‚`‚a‚b‚ًˆّ‚‚ئ
پ ‚j‚`‚b‚gپ{پ ‚a‚e‚f‚bپپپ ‚`‚c‚d‚a
‚·‚ب‚ي‚؟
پ@ ‚پ²پ{‚‚²پپ‚ƒ²
‚ئ‚ب‚éپB