.同じ中心を持つ二つの球があり,小さい球の表面に接しない多面体をより大きな球に内接させる。

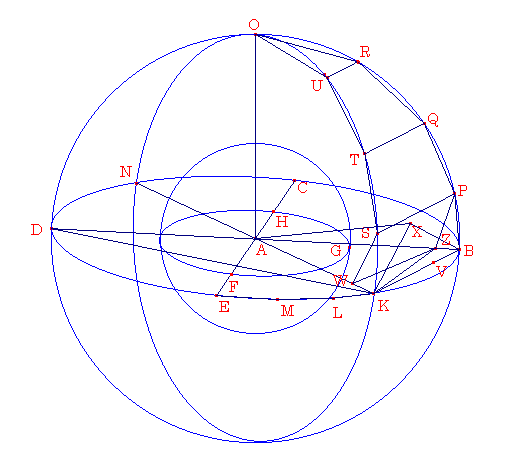
中心を通る何らかの平面によって球を切りとる。すると切断面は円である、なぜなら，直径が固定されたまま半円がうごくことによってできるのが円であるからである。それゆえに、半円があると考えるどんな場所でも、それを通して運ばれた平面は球の表面の上に円をつくる。そしてこの円が、最も大きいのは明白である。なぜならば，円の直径が明らかに半円および直径であり，円あるいは球にひかれたすべての直線より大きいからである。大きい球の円を BCDE とし，小さい球の円ををFGHとする。直角となるように BD と CE を２つの円の直径として引く。それから、同じ中心をもつ２つの円 BCDE と FGH とし,小さい円FGHに接しない，等辺かつ偶数辺である多面体をより大きな球に内接させる。

BEをBK ，KL ，LM と ME が４つにわけるとする。KA を結び、Nまでのばす。点Ａから円 BCDE の平面に直角になるように AO をつくり、そして，球の表面にOで交わる.

AO と直線の BD と KN のそれぞれを通る平面をつくる。それらは先に述べられた理由により球の表面において最も大きい円をつくる。それらをつくるとし，BOD， KON を BD と KN の上の半円であるようにする。今、 OA が円 BCDE の飛行機に直角をなすので、そのために OA とおるすべての平面も円 BCDE の平面にたいして直角をなす。それゆえに，半円BOD， KON は円 BCDE の平面に同じく直角となる。

そして、半円BED、BOD, KON は等しい。なぜなら，それらは等しい直径 BD，KN 上にあるからである。そのために四分円 BE，BO，KO はお互いに等しい。そのため四分円 BE 内にある多角形の辺と同じ数の直線 BK,KL,LM,ME 等しい直線が四分円BO,KOの中にもある。BP,PQ,QR,RO と KS,ST,TU,UO が，それらに内接するとする。SP,TQ,URが結ばれ,そしてＰとＳから円 BCDE の平面に垂線を引くこれらは平面の交線BD,KN上におちるであろう。なぜなら，BOD,KONの平面も円BCDEの平面に直角であるから。おちるものとし，それらPVとSWとし，WVが結ばれたとする.今，等しい半円BODと KON が等しい直線 BP と KSが切り離され、そして垂線PV とＳＷが引かれたので、そのために PV はＳＷは等しく、そして BV はKWに等しい。けれどもＢＡ全体も同じく KA 全体に等しい。そのために残りＶＡは同じく残りＷＡに等しい。そのために、KWがWAに対するように，BV はＶＡに対する。そのために WV はＫＢに対し，平行である。

そして、直線 PV とＳＷのそれぞれが円 BCDEの平面と直角をなすので 、そのために PV がＳＷと平行である。けれどもそれは同じくそれと等しいと証明されました、そのために WV と SP は等しくて、そして平行である。そして、 WV が SP に平行であり、そして WV がＫＢに平行であるので、そのために SP が同じくＫＢに平行である。そしてＢＰと KS の端を結びと、そのために四辺形 KBPS は１つの平面にある。なぜならもし２つの直線が平行し、そして点が，それらのそれぞれの上に任意にとられるなら，点を結んでいる直線は平行線と同じ平面にあるからである。同じ理由のために四辺形SPQT とTQRUのそれぞれが,同じ平面にある。けれども三角形URO は同じく１つの平面にある。もし点Ｐ,Ｓ,Ｑ,Ｔ,Ａから点Aに直線が結ばれたとしたら，弧BO,KOの間に四辺形KBPS ,SPQT,QRU と三角形UROを底面とし、点Ａが 頂点 である角錐から成り立っている多面体が作られるであろう。そして、もし辺KL,LM,MEのそれぞれにも,そしてさらに、残っている３つの四分辺の上にも、BK上におけるのと同じ作図をしたら，これらの四辺形と三角形URO とそれらに対応しているものを底面とし、点Aを頂点とする角錐となり，球に内接するある多面体が作られるであろう。この多面体が円 FGH をふくむ，より小さい球の表面に接しないとする。点Ａから四辺形 KBPS の平面と垂直に交わるようにAXを引き、そして平面と交わる点をXとし，XB と XKを結ぶ。それから、AXが四辺形KBPS の平面に直角をなすので、そのために四辺形の平面にあるすべての直線は直角に交わる。そのためにAXは直線 BX と XKのそれぞれと直角となる。そして、 AB が AK と等しいので，そのために AB の上の正方形は AK の上に正方形に等しい。そしてAXと XB 上の正方形の和は AB の上に正方形に等しい。そしてXにおける角が直角であるから,AXとXK 上の正方形の和は AK の上に等しい。そのためにおのと XB の上の正方形の和はAXと XK の上に正方形の和に等しい。AXの上の正方形が双方から引いたとする。そのために,BX の上の正方形の残りは,XK の上の正方形の残りに等しい。そのために BX は XK に等しい。同様に,XからＰとＳまで結んだ直線が,直線 BX とXKのそれぞれと等しいことを証明することができる。そのために中心をＸとし，BKとXKの一つを半径として描かれた円は,P,Sの両方を通り，KBPSは円の中にある一つの四辺形である。今,KBがWVより大きく、そしてWVとSP等しいから、そのために,KBはSPより大きい。けれどもＫＢが直線KS とＢＰのそれぞれと等しいから、そのために直線KS と等しく,そしてＢＰは SP より大きい。

そして、 KBPS が円の中にある四辺形であり、そしてＫＢ、ＢＰと KS がそれぞれ等しく、そしてPSより小さく、そして BX が円の半径であるので、そのためにＫＢ上の正方形は BX 上の正方形の２倍より大きい。Ｋから BV と垂直に交わる KZ 引く。すると,BD がDZの2倍よりちいさい。そして、BDがDZに対するように，長方形DB，BZが長方形 DZ ，ZDに対するから、そのためにもし正方形が BZ の上に書かれ、そして ZD の上の平行四辺形が完結されたなら,長方形DE,BZは長方形 DZ，ZB の２倍より小さい。そして、もし KD を結んだら、長方形DB,BZは BK の上に正方形と等しい。そして ,長方形 DZ,ZB は KZ の上に正方形と等しい。そのためにＫＢ上の正方形はKZ上の正方形の２倍より小さい。けれどもＫＢ上の正方形は BX の上の正方形の２倍より大きい。そのために KZ の上の正方形は BX の上に正方形より大きい。そして、 BA が KA と等しいので、そのために BA の上の正方形は AK の上に正方形と等しい。そして BX と XA の上の正方形の和は KZ と BA 上の正方形の和と等しい。そして ZA とKA 上の正方形と等しい。そのために BX と XA 上の正方形の和は KZ と ZA の上に正方形の和と等しい。そしてKZ の上の正方形は BX の上の正方形より大きい。そのために残りである、ZA の上の正方形は XA上の正方形より大きい。そのためにAXは AZ より大きい。そのためにAXはＡＧよりさらに大きい。そしてAXは多面体の１つの底面に対して,AGは小さい球の表面に対して,垂直である。したがって,多面体は小さい球の表面に接しない。同じ中心を持つ二つの球があり,小さい球の表面に接しない多面体をより大きな球に内接させる。

しかし,もしもう１つの球を球 BCDEの中の多面体と相似な多面体に内接させると,球BCDEの中の多面体はもう一つの球の中の多面体に対して,球BCDEの直径がもう一つの球の直径に対する三乗の比率となる。なぜなら,立体が同じ数の相似な位置にある角錐に分けられるとき，それらの角錐は相似であるからである。けれども相似な角錐は,それらの対応する辺の三乗の比率となる。そのために四辺形KBPSを底面とし,点Aを頂点とする角錐は,もう一つの球において相似な位置にある角錐に対し,対応する辺が対応する辺に対する。つまり，Aを中心とする球の半径ABがもう一つの球の半径に対して三乗の比率となる。同様にAを中心とする球の中にある角錐は,それぞれもう一つの球の中にある相似な位置にある角錐のそれぞれに対して,ABがもうひとつに球の半径に対する,三乗の比率となる。そして前者の一つが後者の一つに対するように,前者のすべての和が後者のすべての和に対する。それゆえに，Aを中心とする球の中にある多面体の全体は,もう一つの球の中にある多面体全体に対して,ABがもう一つの球の半径に対する。つまり，BDがもう一つの球の直径に対する三乗の比率となる。

　証明終了

第12巻命題16へ　第12巻命題18へ　第12巻目次へ