命題18
球はお互いにそれぞれの直径の
3乗の比率となる。
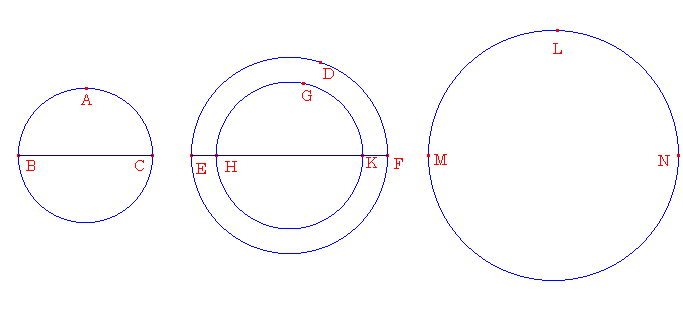
球ABCと
DEF があり、そして BC と EF をそれらの直径とする。球ABCは球DEFに対し BC が EF に対するように3乗の比率となる.もし球ABCが球
DEFに対し,、BC が EF に対するように3乗の比率とならないならば,球ABCは球DEFに対して,BC が EF に対するように3乗より小さいか,あるいは大きい比率となるであろう。最初に、円 GHK より小さい比率とする。DEF
とGHK が同じ中心であるようにする。より大きい球 DEF がその表面において,より小さい球 GHK に接しない多面体を内接させる。同じく,球ABCにも球DEFの中にある多面体に相似な多面体が内接するとする. そのためにABCの中で内接する多面体はDEFの中で内接する多面体に対して BC が EF に対する3乗の比率となる。 しかし,球ABCが球GHKに対して BC が EF に対する3乗の比率となる,そのため,球ABCが球GHKに対するように,ABCの中で内接する多面体がDEFの中で内接する多面体に対する.いれかえると,球ABCがABCの中で内接する多面体に対するように,球GHKがDEFの中で内接する多面体に対する.しかし,球ABCはABCの中で内接する多面体より大きい.それゆえに,球GHKもまた,DEFの中で内接する多面体より大きい.しかし,小さくもある.なぜならば,それに含まれるからである. そのために球ABCが球DEFより小さいものに対して,直径BCがEFに対する3乗の比率とはならない. 同様に球DEFも球ABCより小さいものに対して,EFがBCに対する3乗の比率とはならないことを証明することができる.次に球
ABC が球DEFよりすべて大きくなる,BCがEFに対する3乗の比率があったとする. なぜなら、もし可能であるなら、LMNより大きな比率があることになる.そのために、逆に,球
LMN は球ABCに対して,直径 EF が直径 BC に対する3乗の比率となる. けれども、 LMN が DEF より大きいので、そのために前に証明したように,球 LMNが 球ABCに対するように,球DEFは球ABCより小さなものに対する。そのために球
DEFもまた,球ABCより小さなものに対して,EFがBCに対する3乗の比率となる.これは,不可能であると証明された。そのために球ABC球DEFより大きいすべての球に対して,BCがEFに対する3乗の比率とならない。けれどもまた、より少し球にそれがその比率を持っていることは証明された。そのために球ABCは球DEFに対して,BCがEFに対する3乗の比率となる。ゆえに、球はお互いにそれぞれの直径の3乗の比率となる。証明終了