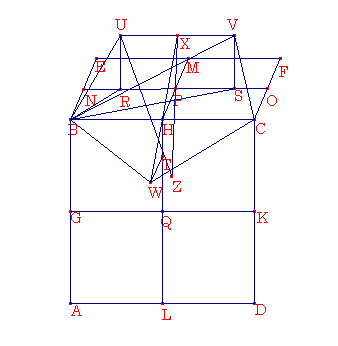
命題17
正十二面体を組み立てて
,そして前述の図形のように,球でそれを囲み,そして正十二面体の辺が余線分という劣線分であることを証明する.
ABCD
とCBEFを,前述の図形のように互いに直角をなす立方体の2つの平面とする. 辺AB,BC,CD,DA,EF,EBのそれぞれを,点G,H,K,L,M,N,Oにおいて2等分し,FC,GK,HL,MH,NOを結ぶ.点R,S,Tにおいて直線NP,PO,HQを外中比で分け,そしてRP,PS,TQを大きい部分とする.点R,S,Tから立方体の面に垂直に立方体の外部に向かってRU,SV,TWを立て,そしてそれらをRP,PS,TQと等しくさせる.UB,BW,WC,CV,VUを結ぶ.五角形UBWCVが等辺で,1つの平面にあり,そして等角であるとする.RB,SB,VBを結ぶ.すると,直線NPがRにおいて外中比に分けられ,そしてRPが大きい部分であるので,そのためにPNとNRの上の正方形の和は,RPの上の正方形の3倍となる.けれども,PNはNBと等しい.そして,PRはPNとNRの上の上の正方形の和と等しい.そのために,NRはRUの上の正方形の3倍である.けれどもBRの上の正方形はBNとNRの上の正方形の和と等しい.そのためにBRの上の正方形はRUの上の正方形の3倍である.そのため,BRとRUの正方形の和は,RUの上の正方形の4倍となる.BUの上の正方形は,BRとRUの上の正方形の和と等しい.そのためにBUの上の正方形の和は,RU の上の正方形の4倍となる.そのために,BUはRUの2倍となる.けれども,VUは同じくPRの,すなわちRUの2倍である.そのために,BUはUVと等しい.同様に,直線BW,WC,CVのそれぞれが,同じく直線BU,UVと等しいことが証明できる.そのために五角形BUVCWは等辺である.次に,それが同じく1つの平面にあることを証明する.Pから直線RUとSVのそれぞれに,立方体の外部に向かって平行にPXを引き,XHとHWが結ばれたとする.XHWが直線であるする.HQがTにおいて外中比に分けられ,そしてQTがその大きい部分であるので,そのためにHQがQTに対するように,QTがTHに対する.けれどもHQがHPと等しい.そしてQTがTWとPXのそれぞれと等しい.そのために,HPがPXに対するように,WTがTHに対する.そしてHPはTWと平行している.なぜならば,それらは平面BDと直角をなしているからである.そして,THはPXと平行している.なぜならば,それらは平面BFと直角をなしいるからであるけれども,もしそれらの対応する辺が同じく平行していて,2つの辺が2つの辺に比例している2つの三角形XPH,HTWが1つの角に結ばれているならば,それから残っている直線は一直線となる.そのために,XHとHWは1つの直線となる.そして,すべての直線が1つの平面にある.そのために五角形UBWCVは,1つの平面にある.次にそれが同じく等角であることを証明する.直線NPがRで外中比に分けられ,PRがその大きい部分であり,PRがRSと等しいので,そのためにNSがPにおいて外中比に分けられ,NPが大きい部分となる.そのために,NSとSPの上の正方形の和は,NPの上の正方形の3倍となる.けれども,NPはNBと等しい.そしてPSがSVと等しい.そのためにNSとSVの上の正方形の和はNBの上の正方形の3倍となる.それゆえに,VS,SN,NBの上の正方形の和は,NBの上の正方形の4倍となる.けれども,SBの上の正方形がSNとNBの上の正方形の和と等しい。そのために,BSとSVの上の正方形の和,つまりBVの上の正方形は,NBの上の正方形の4倍である.そのために,VBはBNの2倍となる.けれども,BCは同じくBNの2倍である.そのために,BVはBCと等しい.そして,2辺BUとUVが2辺BWとWCに等しく,底辺BVが底辺BCと等しい.そのために角BUVは角BWCと等しい.同様に,角UVCが同じく角BWCと等しいことが証明できる.そのために3つの角BWC,BUV,UVCは,互いに等しい.けれども,もし等辺の五角形で3つの角がお互いに等しいならば,五角形は等角となる.そのために五角形BUVCWは等角となる.そしてそれは同じく等辺であると証明された.そのために五角形BUVCWは等辺で,そして等角であり,それは立方体の1辺BCの上にある.そのために,もし立方体の12の辺のそれぞれの上に同じ作図をするならば,12の等辺のであり,等角の五角形によって囲まれる,正十二面体とよばれるものが組み立てられるであろう.次に,それを所定の球で囲み,そして正十二面体の辺が余線分と呼ばれる劣線分であることを証明する。XPを延長し,そしてできた直線をXZとする.すると,PZは対角線と交わり,お互いを二分することは,第11巻の最後のから2番目の定理で証明された.それをZにおいて切るとする.そのためにZは立方体を囲む中心となる.そして,ZPは立方体の辺の2分の1である.UZを結ぶ.今,直線NSがPにおいて外中比に分けられ,そしてNPがそのより大きい部分であるので,NS とSPの上の正方形の和は,NPの上の正方形の3倍となる.けれども,NPはPXと等しく,PZは同じくPRと等しい.そのために,NRはXZと等しい.けれども,PRはRPと等しいから,ZUとも等しい.そのために,ZXとZUの上の正方形の和は,NPの上の正方形の3倍となる.けれども UZ の上の正方形は ZX とZUの上の正方形の和と等しい.そのために,UZの上の正方形は,NPの上の正方形の3倍となる.しかし,立方体を囲む球の上の正方形も,立方体の辺の半分の上の正方形の三倍となる。なぜなら,それは立方体を作図して,そして球でそれを囲み,,そして球の直径の上の正方形が立方体の辺の上の正方形の3倍であることが証明されているからである.けれども,もし全体が全体に対してこのような関係になるならば,半分も同じく半分に対する関係となる.そして NP が立方体の辺の2分の1である.そのために,UZが立方体を囲む球の半径に等しくなる.そしてZは立方体を囲む球の中心である.そのために点Uは球の表面上にある.同様に,正十二面体の残っている角のそれぞれが同じく,球の表面上にあることを証明することができる.そのために,正十二面体は所定の球によって囲まれる.次に,正十二面体の辺が余線分という無理線分であることを証明する.NPが外中比に分けらたとき,RPが大きい部分である.そして,POが外中比に分けられたとき,PRが大きい部分である.よって,NO全体が外中比に分けられたとき,RSが大きい部分となる.そして,NPがPRに対するように,PRがRNに対する.よって,同じ倍数比となるので,2倍のときも同じ関係が成り立つ.そのために,NOがRSに対するように,RS がNRとSOの和に対する.けれども,NOはRSより大きい.そのために,RSがNRとSOの和より大きい.そのために,NOは外中比に分けられ,RSは大きい部分となる.けれども,RSはUVと等しい.よって,NOが外中比に分けられたとき,UVは大きい部分となる.そして,球のの直径が有理線分である.そしてそれの上の正方形が立方体の辺の上の正方形の3倍である.そのために,立方体の辺であるNOは,有理線分である.けれども,もし有理線分が外中比に分けられるならば,その部分はそれぞれ無理線分となるそのためにUVは,余線分という無理線分となる。
系
これから立方体の辺が外中比で分けられるならば
,より大きい部分が正十二面体の辺となることが明らかである.証明終了