柦戣114
乽梋慄暘偲擇崁慄暘偱偱偒偨柺愊偑偁傝擇崁慄暘偺2偮偺崁偑梋慄暘偺2偮偺崁偲捠栺壜擻偱摨偠斾傪帩偮側傜偽偦偺偲偒柺愊偲摍偟偄惓曽宍偺堦曈偼桳棟偱偁傞乿

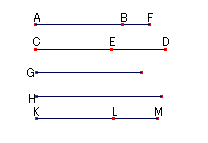
挿曽宍AB,CD偼梋慄暘AB偲擇崁慄暘CD偱偱偒傞偲偟,CE偼CD偺戝偒偄曽偲偟,擇崁慄暘偺崁偺CE,ED偼梋慄暘偺崁AF,FB偲捠栺壜擻偱偁傝摨偠斾傪帩偮偲偡傞丅 偦偟偰挿曽宍AB,CD偵摍偟偄惓曽宍偺堦曈傪G偲偡傞丅
G偑桳棟慄暘偱偁傞偙偲傪帵偡丅
H傪桳棟慄暘偲偟,H忋偵H忋偺惓曽宍偵摍偟偔KL傪暆偲偡傞挿曽宍CD傪偮偔傞丅偙偺偲偒KL偼梋慄暘偱偁傞丅
KM偲ML偼擇崁慄暘偺崁CE,ED偲捠栺壜擻偱偁傝,摨偠斾傪帩偮偲偡傞丅嘳.112
偟偐偟CE,ED偼AF,FB偲捠栺壜擻偱摨偠斾傪帩偮丅傛偭偰AF偑FB偵懳偡傞傛偆偵KM偑ML偵懳偡傞丅
傛偭偰偄傟偐偊偰AF偑KM偵懳偡傞傛偆偵BF偑LM偵懳偡傞丅傛偭偰巆傝偺AB偑巆傝偺KL偵懳偡傞傛偆偵AF偑KM偵懳偡傞丅 嘪.19
偙偙偱AF偼KM偲捠栺壜擻,傛偭偰AB傕KL偲捠栺壜擻偱偁傞丅 嘳.12 嘳.11
偦偟偰丆AB偑KL偵懳偡傞傛偆偵挿曽宍CD,AB偑挿曽宍CD,KL偵懳偡傞丅傛偭偰挿曽宍CD,AB偼挿曽宍CD,KL偲捠栺壜擻偱偁傞丅 嘫.1 嘳.11
偙偙偱挿曽宍CD,KL偼H忋偺惓曽宍偵摍偟偄丅傛偭偰挿曽宍CD,AB偼H忋偺惓曽宍偲捠栺壜擻偱偁傞丅
傑偨丆G忋偺惓曽宍偼挿曽宍CD,AB偵摍偟偄丅傛偭偰G忋偺惓曽宍偼H忋偺惓曽宍偲捠栺壜擻偱偁傞丅
偙偙偱H忋偺惓曽宍偼桳棟偱偁傞丅傛偭偰G忋偺惓曽宍傕桳棟偱偁傞丅
傛偭偰G偼桳棟偱偁傞丅偦偟偰偦傟偼挿曽宍CDAB偵摍偟偄惓曽宍偺堦曈偱偁傞丅
偟偨偑偭偰丆梋慄暘偲擇崁慄暘偱偱偒偨柺愊偑偁傝擇崁慄暘偺2偮偺崁偑梋慄暘偺2偮偺崁偲捠栺壜擻偱摨偠斾傪帩偮側傜偽偦偺偲偒柺愊偲摍偟偄惓曽宍偺堦曈偼桳棟偱偁傞丅
徹柧廔椆
偦偟偰桳棟柺愊偑柍棟慄暘偵傛偭偰偱偒傞偙偲偑壜擻偱偁傞偲偄偆偙偲偑柧傜偐偵側偭偨丅