命題10
どんな円柱でも同じ底面
,そして等しい高さを持っている円柱の3分の1となる.
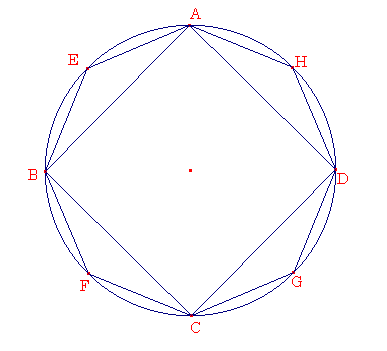
円
ABCDを底面とする,等しい高さの円錐と円柱があったとする.円錐が円柱の3分の1であり,円柱が円錐の3倍あることを求める.なぜなら,もし円柱が円錐の3倍ではないなら,円柱は円錐より,3分の1より大きいか,3倍より小さくなる.まず,3分の1より大きいとする.円ABCDに正方形ABCDを内接させる.正方形ABCDは円ABCDの2分の1より大きい.正方形ABCDを底面とする,円柱と等しい高さの角柱をつくる.作られた角柱は,円柱の半分より大きい.なぜならば,もし円ABCDに正方形が外接してるならば,内接した正方形は外接したものの2分の1となる.そして,その上につくられた平行六面体は,同じ高さの角柱なのである.しかし,同じ高さの平行六面体は底面に対する.よって,正方形ABCDの上の角柱は正方形ABCDに外接する角柱の2分の1となる.そして,円柱は円ABCDに外接する正方形の上の角柱より小さい.よって,正方形ABCDの上の円柱と同じ高さの角柱は,円柱の2分の1より大きい.円周AB,BC,CD,DAを点E,F,G,Hで2等分し,AE,EB,BF,FC,CG,GD,DH,HAを結ぶ.そして,前に証明したように,三角形AEB,BFC,CGD,DHAのそれぞれは,円ABCDのその切片の半分より大きい.三角形AEB,BFC,CGD,DHAの上に,円柱と等しい高さの角柱をつくる.すると,つくられた角柱は円柱のそれぞれを含む切片の2分の1より大きい.なぜならば,点E,F,G,Hを通り,AB,BC,CD,DAに平行線を引き,AB,BC,CD,DAの上の平行四辺形を作り,その上に円柱と同じ高さの平行六面体を作るならば,三角形AEB,BFC,CGD,DHAの上の角柱は立てられた立体の2分の1となる.そして円柱の切片は作られた平行六面体より小さい.よって,三角形AEB,BFC,CGD,DHAの上の角柱は円柱のそれぞれを含む切片の2分の1より大きい.そして,残っている周を二分し,直線を結び付けて,三角形のそれぞれの上に円柱と等しい高さの角柱を作り,そしてこれを繰り返して,円柱と角錐の3倍との差より小さい.残ったものを,AE,EB,BF,FC,CG,GD,DH,HAとする.そのために,多角形AEBFCGDHを底面とし同じ高さの残りの角柱は円錐の3倍より大きい.けれども多角形AEBFCGDHを底面とする,円柱と同じ高さの角柱は多角形AEBFCGDHを底面とする,円錐と同じ頂点の角錐の3倍である.そのために,多角形AEBFCGDHを底面とし,円錐と同じ頂点を持つ角錐は円ABCDを底面とする円錐より大きい.けれども,それは同じくより小さくもる.そしてそれは不可能である.そのために円柱はコーンの3倍より大きくありません。次に,円柱が円錐の3倍より小さくもないことを求める.なぜなら,もし可能であるなら,円柱を円錐3倍より小さいとする.そのために,逆に,円錐は円柱の3倍より大きいことになる.円ABCDに正方形ABCDを内接させる.そのために,正方形ABCDは円ABCDの半分より大きい.正方形ABCDの上に円錐と同じ頂点をもつ角錐をつくる.そのために,つくられた角錐は,円錐の2分の1より大きい.なぜなら,前に証明したように,もし,円に正方形を外接させたら,正方形ABCDは円に外接する正方形の2分の1となる.そして,もし,正方形の上に円錐とおな次高さの,角柱と呼ばれる平行六面体を作るならば,正方形ABCDの上の角柱は円に外接する角柱の2分の1である.なぜなら,それらは底面に比例するからである.そにために,それらの3分の1は同じくその比率となる.そのために,正方形ABCDを底面とする円柱は円に外接した正方形の上に作られた円柱の2分の1となる.そして,円に外接した正方形の上の角錐は円錐を含むから,それより大きくなる.そのために,正方形ABCDを底面とする角柱は,同じ頂点をもつ円錐の2分の1より大きい.弧AB,BC,CD,DAを点E,F,G,Hで2等分し,AE,EB,BF,FC,CG,GD,DH,HAを結ぶ.そして,三角形AEB,BFC,CGD,DHAのそれぞれは,円ABCDの,それぞれを含む切片の半分より大きい.今,三角形AEB,BFC,CGD,DHAの上に,円錐と同じ頂点をもつ角錐をつくる.そのために,つくられた角錐のそれぞれはも同じ方法で円錐の,それぞれをふくむ切片の半分より大きい.そして,残っている弧を二分して,直線を結び付けて,三角形のうえに円錐と同じ頂点をもつ角錐を作り,そして繰り返してこれをすることによって,円錐と円柱の3分の1との差より小さい何らかの円錐の切片が残ると思われる.そして,残ったものをAE,EB,BF,FC,CG,GD,DH,HA の上にあるようにする.そのために,多角形AEBFCGDHを底面とする,円錐と同じ高さを持つ残りの角錐は円柱の3分の1となる.けれども,多角形AEBFCGDHを底面とする,円錐と同じ高さを持つ角錐は,多角形AEBFCGDHを底面とし,円柱と同じ高さの角柱の3分の1である.よって,多角形AEBFCGDHを底面とし,円柱と同じ高さの角錐は円ABCDを底面とする円柱より大きい.けれどもそれは,それに含まれるから,小さくもある.そしてそれは不可能である.そのために,円柱は円錐3倍より小さくもない.けれども,それが3倍より大きくないことは証明された.そのために円柱は,円錐の3倍であり,そのため,円錐は円柱の3倍となる.そのために,どんな円柱でも同じ底面,そして等しい高さを持っている円柱の3分の1となる.証明終了