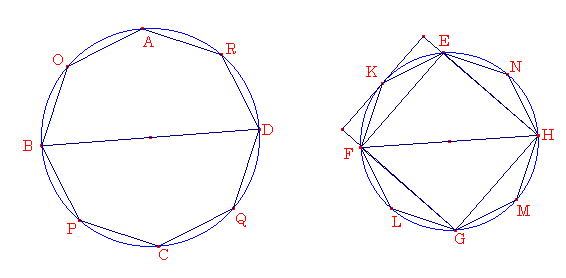
命題2
円はそれらの直径の上の正方形と比例する
.
ABCD
とEFGHを円とし,そしてBDとFHをそれらの直径とする.円ABCDが円EFGHに対するように,BDの上の正方形がFHの上の正方形に対することを求める.もし,BDの上の正方形がFHの上の正方形に対するように,円ABCDが円EFGHに対するとしないならば,BDの上の正方形がFHの上の正方形に対するように,円ABCDは円EFGHより小さい面積か,大きい面積に対するであろう.まず,小さい面積Sに対するとする.円EFGHに正方形EFGHを内接させる.すると,内接している正方形は円EFGHの半分より大きい.なぜなら,もし点E,F,G,Hを通る円の接線を引くならば,正方形EFGHは円に外接した正方形の半分となる.そして,円は外接している正方形より小さい.そのため,外接した正方形EFGHが円EFGHの半分より大きい.円周EF,FG,GHを二等分する.その点をK,L,M,Nとし,EK,KF,FL,LG,GM,MH,HN,NEを結ぶ.すると,三角形EKF,FLG,GMH,HNEはそれぞれ,それをふくむ切片の半分より大きくなる.なぜならば,点K,L,M,Nを通る円の切片を引き,線分EF,FG,GH,HEの上に平行四辺形をつくるならば,三角形EKF,FLG,GMH,HNEはそれぞれ,それをふくむ平行四辺形の半分となる.そして,それをふくむ切片は平行四辺形より小さいので,三角形EKF,FLG,GMH,HNEはそれをふくむ切片の半分より小さい.それで,残っている円周を二等分して,そして直線を結ぶことを繰り返すと,円EFGHと面積Sとの差より非常に小さな円の切片が残るであろう.なぜならば,2つの違う量を決め,もし大きいものからその半分より大きい量を取り除き,さらに残ったもののから半分より大きいものを取り除いていくことを,繰り返すと,最初に決めた小さいほうの量より小さい量のものが残るということを,第10巻第1定理において証明されているからである.そこで,円EFGHのEK,KF,FL,LG,GM,MH,HN,NEの切片が,円EFGHと面積Sより小さいものとする.そのために残りの多角形EKFLGMHN面積Sより大きい.今,円ABCDに多角形EKFLGMHNと相似な多角形AOBPCQDRが内接してるとする.そのために,BDの上の正方形がFHの上の正方形に対するように,多角形AOBPCQDRが多角形EKFLGMHNに対する.けれども,BDの上の正方形はFHの上の正方形に対するように,円ABCDが面積Sに対する.そして,円ABCDが面積Sに対するように,多角形AOBPCQDRが多角形EKFLGMHNに対する.そのために,いれかえると,円ABCDがその中に内接した多角形に対するように,面積Sが多角形EKFLGMHNに対する.けれども,円ABCDはその中に内接した多角形より大きい.そのために面積Sは多角形EKFLGMHNより同じく大きい.けれども,それは同じく小さい.それは不可能である.そのために,BDの上の正方形がFHの正方形に対するように,円ABCDが円EFGHより小さい面積に対することはありえない.同様に,FHの上の正方形がBDの上の正方形に対するように,円EFGHが円ABCDより小さい面積にたいすることがありえないことも証明できる.次に,BDの上の正方形がFHの上の正方形に対するように,円ABCDが円EFGHより大きい面積に対することがありえないことを考える.なぜなら,もし可能であるなら,それをより大きい面積Sに対するとする.そのために,逆にすると,FHの上の正方形がDBの上の正方形に対するように,面積Sが円ABCDに対する.けれども,これは不可能であることが証明されている.そのために,BDの上の正方形がFHの上の正方形に対するように,円ABCDが円EFGHに対する.よって,円はそれらの直径の上の正方形と比例する.
補助定理
面積
Sが円EFGHより大きいとき,面積Sが円ABCDに対するように,円EFGHが面積Sより小さい面積に対することを求める.面積Sが円ABCDに対するように,面積Tが円EFGHに対するとする.面積Tが円ABCDより小さいことを求める.よって,面積Sが円ABCDに対するように,円EFGHが面積Tに対する.言いかえると,面積Sが円EFGHに対するように,面積Tが円ABCDに対する.しかし,面積Sは,円EFGHより大きい.よって,円ABCDは,面積Tより大きい.そのために,面積Sが円ABCDに対するように,円EFGHが円ABCDより小さい面積に対する.そのために,円はそれらの直径の上の正方形に比例する.証明終了