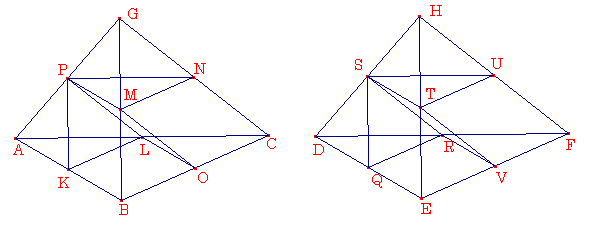
命題4
もし三角形を底辺とし
,同じ高さの2つの円錐があったとする.そして,それぞれが等しく,そしてお互いに類似していて,全体に類似している2つの角錐と2つの等しい円柱に分けられるなら,1つの角錐の底面がもう1つの角錐の底面に対するように,1つの角錐内の角柱の和がもう1つの角柱の和に対する.
底辺を三角形
ABC,DEFとし,点G,Hを頂点とする高さが同じ角錐があったとする.それぞれが等しく,全体と相似である,2つの角錐と,2つの等しい角柱に分けられたとする.角錐ABCDの中の角柱の和が,角錐DEFHの中の同じ数の角柱の和と等しいことを求める. BOがOCと等しい.そしてALがLCと等しいので,そのためにLOはABと平行である.そして,三角形ABCは三角形LOCと類似である.同じく,三角形DEFは三角形RVFと類似である.そして,BCがCOの,EFはFVの2倍であるから,BCがCOに対するように,EFがFVに対する.そして,BC,COの上に記述されるABCとLOCが相似であり,相似な位置にある.そして,EFとFVの上に同じくDEFとRVFが描かれた.そのために,三角形ABCがDEFに対するように,三角形LOCがRVFに対する.そのために,言いかえると,三角形ABCがDEFに対するように,三角形LOCがRVFに対する.けれども,三角形LOCは三角形RVFに対するように,三角形LOCを底面とし,PMNを対面とする角柱は,三角形RVFを底面とし,STUを対面とする角柱に対する.そのために三角形ABCが三角形DEFに対するように,三角形LOCを底面とし,PMNを対面とする角柱は,三角形RVFを底面とし,STUを対面とする角柱に対する.けれども,2つの角柱のそれぞれが,対するように,平行四辺形KBOLを底面とし,直線PMをそれに対する辺とする角錐は,平行四辺形QEVRを底面とし,それに対する辺をSTとする角錐に対する.そのために2つの角柱,つまり,平行四辺形KBOLを底面とし,OCをそれに対する辺とする角柱と,三角形LOCを底辺とし,PMNを対面とする角柱との和が,QEVRを底面とし,直線STをそれに対する辺とする角柱と,三角形RVFを底面とし,STUを対面とする角柱との和に対して,比例する.そのために,底面ABCがDEFに対するように,その2つの角柱の和がもう2つの角柱の和に対する.そして同様に,もし角錐PMNGとSTUHが2つの角柱2つ角錐に分けられるなら,底面PMNがSTUに対するように,角錐PMNGは角錐STUHに対する.けれども,底面PMNが底面STUに対するように,底面ABCが底面DEFに対する.なぜならば,三角形PMNとSTUのそれぞれが,三角形LOCとRVFと等しいからである.そのために,底面ABCが底面DEFに対するように,4つの角柱の和が,4つの角柱の和に対する.そして同様に,もし三角形を底辺とし,同じ高さの2つの円錐があったとする.そして,それぞれが等しく,そしてお互いに類似していて,全体に類似している2つの角錐と2つの等しい円柱に分けられるなら,1つの角錐の底面がもう1つの角錐の底面に対するように,1つの角錐内の角柱の和がもう1つの角柱の和に対する.
補助定理
三角形
LOCが三角形RVFに対するように,三角形LOCを底面とし,PMNを対面とする角柱は三角形RVFを底面とし,STUを対面とする角柱に対することを,証明する.同じ作図で,GとHから平面ABCとDEFに垂線が引かれたとする.これらは,角錐の定理より,等しい高さである.今,2つの直線GCとGからの垂直なものが,平行した平面ABCとPMNによって切られるので,そのために,それらは同じ比率で切られる.そして,GCはNにおいて平面PMNによって二分される.そのために,Gから平面ABCへの垂線も同じく平面PMNによって二分される.同じく,Hから平面DEFへの垂線も,平面STUによって二分される.そして,GとHから平面ABCとDEFへの垂線も等しい.そのために,三角形PMN,STUから三角形ABC,DEFへの垂線も等しい.そのために,三角形LOCとRVFを底面とし,PMNとSTUを対面とする角柱は,等しい高さである.そのため,この角柱を含む平行六面体は高さが等しく,それぞれに底面に比例する.そして,それらの半分であるこの角柱は底面LOCが底面RVFに対する.よって,三角形LOCが三角形RVFに対するように,三角形LOCを底面とし,PMNを対面とする角柱は三角形RVFを底面とし,STUを対面とする角柱に対する.証明終了