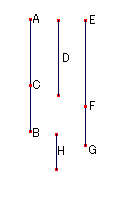
命題51
第四の二項線分を見つける。

二つの数をAC,CBとし,ABはBCともACとも 平方数が平方数に対する比をもたないとする。
有理線分をDとし,EFはDと長さにおいて通約可能とする。
このとき,EFも有理線分である。
EF上の正方形がFG上の正方形に対するように,数BAがACに対する。
そのとき,EF上の正方形はFG上の正方形と通約可能である。 よって,FGも有理である。 Ⅹ.6.Cor. Ⅹ.6
ここで,BAはACと平方数が平方数に対する比をもたないので,
EF上の正方形もFG上の正方形と平方数が平方数に対してもつ比をもたない。
よって,EFはFGと長さにおいて通約不可能である。 Ⅹ.9
よってEFとFGは平方においてのみ通約可能な有理線分であり, EGは二項線分である。
次に,EGが第四の二項線分であることを示す。
BAがACに対するように,EF上の正方形がFG上の正方形に対するので,
EF上の正方形はFG上の正方形より大きい。
FG上の正方形とH上の正方形の和は, EF上の正方形と等しいとする。
このとき,除比の理より,数ABがBCに対するように, EF上の正方形がH上の正方形に対する。 Ⅴ.19.Cor.
しかし,ABはBCに対して平方数が平方数に対する比をもたない。
よって,EF上の正方形もH上の正方形に対して, 平方数が平方数に対する比をもたない。
よって,EFもHと長さにおいて通約不可能。
よって,EF上の正方形はGF上の正方形より, EFと通約不可能な直線上の正方形だけ大きい。 Ⅹ.9
EFとFGは平方においてのみ通約可能な有理線分で, EFはDと長さにおいて通約可能である。
よって,EGは第四の二項線分である。