命題52
第五の二項線分を見つける。

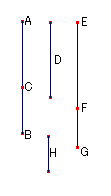
二つの数をAC,CBとおき,ABはそれらに対して 平方数が平方数に対する比を持たないとする。
ある有理線分をDとおき,EFはDと通約可能とする。
このときEFは有理線分である。
CAがABに対するようにEF上の正方形がFG上の正方形に対するとする。 Ⅹ.6.Cor.
CAはABに対して平方数が平方数に対して持つ比を持たない。
よって,EF上の正方形はFG上の正方形に対して 平方数が平方数に対して持つ比を持たない。
ゆえに,EFとFGは平方においてのみ通約可能な有理線分である。
次に,第五の二項線分であることを示す。
CAがABに対するようにEF上の正方形がFG上の正方形に対するので,
逆に,BAがACに対するようにFG上の正方形がFE上の正方形に対する。
よって,GF上の正方形はFE上の正方形より大きい。 Ⅴ.7.Cor.
また,EFとH上の正方形の和がGF上の正方形と等しいとする。
このとき,除比の理より,数ABがBCに 対するようにGF上の正方形はH上の正方形に対する。 Ⅴ.19.Cor.
またABはBCに対して平方数が平方数に対する比を持たない。
よって,FG上の正方形はH上の正方形に対して, 平方数が平方数に対する比を持たない。
ゆえに,FGはHと長さにおいて通約不可能である。
したがって,FG上の正方形はFE上の正方形より FGと通約不可能な線分上の正方形だけ大きい。 Ⅹ.9
また,GF,FEは平方においてのみ通約可能な有理線分であり,
小さい項EFは定められた
有理線分Dと長さにおいて通約可能である。
よって,EGは第五の二項線分である。
証明終了