柦戣26
拞崁柺愊偼桳棟柺愊偩偗拞崁柺愊傪挻偊側偄

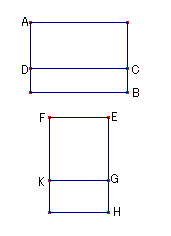
拞崁柺愊AB偑桳棟柺愊DB偩偗拞崁柺愊AC傪 偙偊傞偙偲偑偱偒傞偲偡傞丅
桳棟側捈慄傪EF偲偍偔丅
挿曽宍AB偵摍偟偔丆EH傪暆偲偡傞挿曽宍FH偑EF忋偵偮偔傜傟傞丅
挿曽宍AC偵摍偟偄挿曽宍FG傪FH偐傜傂偔丆
偦偆偡傞偲巆傝偺BD偼巆傝偺KH偵摍偟偄丅
DB偼桳棟偱丆備偊偵KH傕桳棟偱偁傞丅
挿曽宍AB偲AC偼偦傟偧傟拞崁柺愊側偺偱丆
AB偑FH偵摍偟偄傛偆偵AC偑FG偵摍偟偔丆
備偊偵挿曽宍FH偲FG傕偦傟偧傟拞崁柺愊偱偁傞丅
偦傟傜偼桳棟慄暘EF忋偵偮偔傜傟偰偄傞丅
備偊偵丆捈慄HE偲EG偼桳棟偱偁傝丆 FE偲偦傟偧傟挿偝偵偍偄偰捠栺晄壜擻偱偁傞丅 嘳.22
DB 偼桳棟偱丆KH偵摍偟偄偺偱備偊偵KH傕桳棟偱偁傞丅
偦偟偰丆偦傟偼桳棟慄暘EF偱偮偔傜傟偰偄傞丅
備偊偵GH偼桳棟偱EF偲挿偝偵偍偄偰捠栺壜擻偱偁傞丅
嘳.20
EG傕桳棟偱丆EF偲挿偝偵偍偄偰捠栺晄壜擻丅
備偊偵丆EG偼GH偲挿偝偵偍偄偰捠栺晄壜擻丅 嘳.13
傑偨丆EG偑GH偵懳偡傞傛偆偵EG偱偱偒偨惓曽宍偼
EG偲GH偱偱偒偨挿曽宍偵懳偡傞偺偱丆
EG偱偱偒偨惓曽宍偼EG偲GH偱偱偒偨挿曽宍偲捠栺晄壜擻偱偁傞丅
嘳.11
EG偲GH偱偱偒偨惓曽宍偺榓偼EG偱偱偒偨惓曽宍偲捠栺壜擻偱偁傝丆
椉曽偲傕桳棟偱偁傞丅
EG偲GH偱偱偒偨挿曽宍偺擇攞偼 EG偲GH偱偱偒偨挿曽宍偲捠栺壜擻偱偁傞丅 嘳.6 嘳.13
備偊偵丆EG偲GH偱偱偒偨惓曽宍偺榓偼丆 EG偲GH偱偱偒偨挿曽宍偺擇攞偲捠栺晄壜擻偱偁傞丅
備偊偵丆EG偲GH偱偱偒偨惓曽宍偺榓偲EG偲GH偱偱偒偨挿曽宍偺擇攞傪壛偊偨傕偺丆
偮傑傝EH偱偱偒偨惓曽宍偼EG偲GH偱偱偒偨惓曽宍偺榓偲捠栺晄壜擻偱偁傞丅
嘦.6
嘳.16
傑偨丆EG偲GH偱偱偒偨惓曽宍偺榓偼桳棟偱
備偊偵丆EH偱偱偒偨惓曽宍偼柍棟偱偁傞丅
備偊偵丆E俫偼柍棟
偟偐偟丆桳棟偱傕偁傞偺偱柕弬
嘳.Def.4
傛偭偰丆FH偑HK偵懳偡傞傛偆偵丆HK偼KL偵懳偡傞丅
偟偨偑偭偰丆FK丆KL偱偱偒偨挿曽宍偼HK忋偺惓曽宍偵摍偟偄丅 嘫.1 嘪.11 嘫.17
傑偨丆FH,KL偱偱偒偨挿曽宍偼桳棟柺愊偱偁傞丅
備偊偵丆HK忋偺惓曽宍偼桳棟柺愊偱偁傞丅
傛偭偰丆HK偼桳棟慄暘偱偁傞丅
HK偑FG偲挿偝偵偍偄偰捠栺壜擻側傜偽丆
HN偼桳棟柺愊偱
HK偑FG偲挿偝偵偍偄偰捠栺晄壜擻側傜偽丆
KH丆HM偼惓曽宍偩偗偵偍偄偰捠栺壜擻側桳棟慄暘偱偁傞丅
傛偭偰丆HN偼桳棟柺愊偐拞崁柺愊偱偁傞丅
傑偨丆HN偼AC偵摍偟偄丅
傛偭偰丆AC偼桳棟柺愊偐拞崁柺愊偐偺偳偪傜偐偱偁傞丅
徹柧廔椆