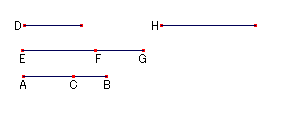
命題48

第一の二項線分を見つける

ACとCBを二つの数であるとする。

それらの和ABはBCに対して平方数であらわせる比を持つ。

しかし，CAに対しては平方数であらわせる比を持たないとする。 �].28.Lemma1

ある有理線分をDとし，EFはDと長さにおいて通約可能であるとする。

ゆえに，EFも有理線分である。

数BAが数ACに対するように EF上の正方形がFG上の正方形に対するようにGをとる。 �].6.Cor.

また，ABはACに対して数であらわせる比を持ち，
ゆえに，EF上の正方形も またFG上の正方形に対して数であらわせる比を持つ。

すなわち，EF上の正方形はFG上の正方形と通約可能である。 �].6

また，EFは有理で，ゆえにFGも有理。

そしてBAはACに対して平方数であらわせる比を持たないので
同様にEF上の正方形は FG上の正方形に対して平方数であらわせる比を持たない。

ゆえに，EFはFGと長さにおいて通約不可能 �].9

したがって，EFとFGは平方においてのみ通約可能な有理線分である。
ゆえに，EGは二項線分である。 �].36

これが第一の二項線分であることを示す。

数BAが数ACに対するようにEF上の正方形がFG上の正方形に対するので，
BAがACより大きい時， EF上の正方形もまたFG上の正方形より大きい。

FG上の正方形とH上の正方形の和がEF上の正方形に等しいとする。

BAがACに対するようにEF上の正方形はFG上の正方形に対するので，
ゆえに，除比の理より，ABがBCに対するように， EF上の正方形はH上の正方形に対する。 �X.19.Cor.

また，ABはBCに対して平方数であらわせる比をもつので，
ゆえに，EF上の正方形はH上の正方形に対して， 平方数であらわせる比を持つ。

したがって，EFとHは長さにおいて通約可能である。

ゆえに，EF上の正方形はFG上の正方形より EFと通約可能な線分H上の正方形だけ大きい。 �].9

また，EFとFGは有理で，EFはDと長さにおいて通約可能である

したがって，EGは第一の二項線分である。

証明終了