柦戣47
擇偮偺拞崁柺愊偺榓偵摍偟偄曈偼丆堦揰偩偗偱暘妱偝傟傞丅

AB偼C偱暘妱偝傟傞偲偡傞丅
AC偲CB偼暯曽偵偍偄偰捠栺晄壜擻偱
AC忋丆CB忋偺惓曽宍偺榓偼拞崁偲偟丆
挿曽宍AC丆CB偼拞崁偱
AC忋丆CB忋偺惓曽宍偺榓偲捠栺晄壜擻偲偡傞丅
AB偼梌偊傜傟偨忦審傪枮偨偡傛偆側 傕偆堦偮偺揰偱暘妱偝傟側偄偙偲傪帵偡丅
壜擻側傜偽AB傪D偱暘妱偡傞丅
偦偟偰丆AC偼BD偲摍偟偔側偔丆AC偺傎偆偑戝偒偄偲偡傞丅
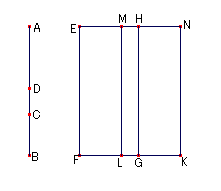
EF傪桳棟慄暘偲偟丆EF偼AC忋丆CB忋偺惓曽宍偺榓偲
摍偟偄挿曽宍EG偵摉偰偼傑傝丆
挿曽宍HK偼挿曽宍AC丆CB偺擇攞偲摍偟偄丅
偙偺偲偒慡懱偺EK偼AB忋偺惓曽宍偲摍偟偄丅 嘦.4
傑偨AD忋丆DB忋偺惓曽宍偺榓偵摍偟偄EL偼EF忋偵偁傞丅
偙偺偲偒巆傝挿曽宍AD丆DB偺擇攞偼巆傝偺MK偵摍偟偄丅
偦偟偰壖掕傛傝丆AC忋丆CB忋偺惓曽宍偺榓偼拞崁丅
傛偭偰EG傕拞崁偱偁傞丅
偦偟偰丆桳棟慄暘EF偵摉偰偼傑傞丅
傛偭偰HE偼桳棟偱EF偲挿偝偵偍偄偰捠栺晄壜擻偱偁傞丅
嘳.22
摨條偵偟偰丆HN偼桳棟偱EF偲挿偝偵偍偄偰捠栺晄壜擻偱偁傞丅
偦偟偰AC忋丆CB忋偺惓曽宍偺榓偼挿曽宍AC丆CB偺擇攞偲捠栺晄壜擻側偺偱
EG傕HK偲捠栺晄壜擻丅
偦偟偰EH傕HN偲捠栺晄壜擻偱偁傞丅
嘫.1
嘳.11
偦偟偰偦傟傜偼桳棟側偺偱 EH偲HN偼暯曽偵偍偄偰偺傒捠栺壜擻側桳棟慄暘偱偁傞丅
傛偭偰丆EN偼H偱暘妱偝傟偨擇崁慄暘偱偁傞丅 嘳.36
摨偠傛偆偵M偱傕暘妱偝傟傞偙偲偑徹柧偱偒傞丅
偦偟偰EH偼MN偲摍偟偔側偄丅
傛偭偰丆擇崁慄暘偼堎側傞擇揰偱暘妱偝傟偨丅
偟偐偟偙傟偼晄崌棟偱偁傞丅
嘳.42
傛偭偰擇偮偺拞崁柺愊偺榓偲摍偟偄曈偼堎側傞揰偱暘妱偝傟側偄丅
傛偭偰堦揰偩偗偱暘偗傜傟傞丅
徹柧廔椆