柦戣87
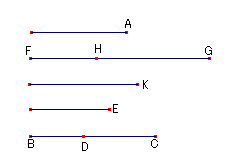
乽戞3偺梋慄暘傪尒偮偗傞乿

E偑BC偵懳偡傞傛偆偵A忋偺惓曽宍偑FG忋偺惓曽宍偵懳偡傞偺偱A忋偺惓曽宍偼FG忋偺惓曽宍偲捠栺壜擻偱偁傞丅 嘳.6
偙偙偱A忋偺惓曽宍偼桳棟丆傛偭偰FG忋偺惓曽宍傕桳棟丅傛偭偰FG偼桳棟偱偁傞丅
E偼BC偵懳偟偰暯曽悢偑暯曽悢偵懳偟偰帩偮斾傪帩偨側偄偺偱A忋偺惓曽宍偼FG忋偺惓曽宍偵懳偟偰暯曽悢偑暯曽悢偵懳偟偰帩偮斾傪帩偨側偄丅 傛偭偰A偼FG偲挿偝偵偍偄偰捠栺晄壜擻偱偁傞丅 嘳.9
偦偟偰椉曽偲傕桳棟側偺偱FG偲GH偼暯曽偵偍偄偰偺傒捠栺壜擻側桳棟慄暘偱偁傞丅傛偭偰FH偼梋慄暘偱偁傞丅 嘳.73
師偵,FH偑戞嶰偺梋慄暘偱偁傞偙偲傪帵偡丅
E偑BC偵懳偡傞傛偆偵A忋偺惓曽宍偑FG忋偺惓曽宍偵懳偡傞偺偱BC偑CD偵懳偡傞傛偆偵FG忋偺惓曽宍偑HG忋偺惓曽宍偵懳偡傞丅傛偭偰摍娫妘斾偵傛傝,E偑CD偵懳偡傞傛偆偵A忋偺惓曽宍偼HG忋偺惓曽宍偵懳偡傞丅 嘪.22
傛偭偰FG傕GH傕桳棟慄暘A偲挿偝偵偍偄偰捠栺晄壜擻偱偁傞丅
偙偙偱FG忋偺惓曽宍偼GH忋偺惓曽宍傛傝K忋偺惓曽宍偩偗戝偒偄偲偡傞丅
BC偑CD偵懳偡傞傛偆偵FG忋偺惓曽宍偑GH忋偺惓曽宍偵懳偡傞丅傛偭偰斀揮斾偵傛傝BC偑BD偵懳偡傞傛偆偵FG忋偺惓曽宍偑K忋偺惓曽宍偵懳偡傞丅
偙偙偱BC偼BD偵暯曽悢偑暯曽悢偵懳偟偰帩偮斾傪帩偮偺偱FG忋偺惓曽宍傕K忋偺惓曽宍偵暯曽悢偑暯曽悢偵懳偟偰帩偮斾傪帩偮丅
偦偟偰FG傕GH傕桳棟慄暘A偲挿偝偵偍偄偰捠栺晄壜擻側偺偱FH偼戞嶰偺梋慄暘偱偁傞丅 嘳.Def.嘨.3
徹柧廔椆