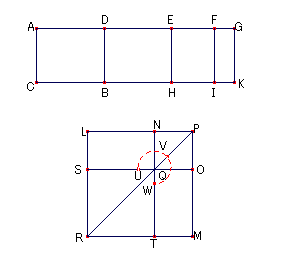
柦戣94
乽柺愊偑桳棟慄暘偲戞4偺梋慄暘偵傛偭偰埻傑傟傞側傜偽丄
偦偺柺愊偵摍偟偄惓曽宍偺曈偼楎慄暘偱偁傞乿

柺愊AB偼桳棟慄暘AC偲戞4偺梋慄暘偵傛偭偰埻傑傟傞偲偡傞丅
柺愊AB偵摍偟偄惓曽宍偺曈偼楎慄暘偱偁傞偙偲傪帵偡丅
AG偼桳棟慄暘偱AC偲挿偝偵偍偄偰捠栺壜擻側偺偱丄慡懱AK偼桳棟柺愊偱偁傞丅 嘳.19
傑偨丄DG偼AC偲挿偝偵偍偄偰捠栺晄壜擻側偺偱DG,AC偼桳棟慄暘偱偁傞丅傛偭偰丄DK偼拞崁柺愊偱偁傞丅 嘳.21
傑偨丄AF偼FG偲挿偝偵偍偄偰捠栺晄壜擻側偺偱AI偼FK偲捠栺晄壜擻偱偁傞丅 嘫.1 嘳.11
AI偵摍偟偄惓曽宍LM偑偮偔傜傟偨偲偟丄FK偵摍偟偔LM偲嫟捠偺妏LPM傪傕偮惓曽宍NO偑傂偐傟偨偲偡傞丅
傛偭偰丄惓曽宍LM,NO偼摨偠懳妏慄傪偼偝傫偱偄傞丅 丂PR偼偦傟傜偺懳妏慄偲偟偰嶌恾偝傟偨偲偡傞丅 嘫.26
挿曽宍AF,FG偼EG偱偱偒偨惓曽宍偵摍偟偄偺偱丄AF偑EG偵懳偡傞傛偆偵EG偑FG偵懳偡傞丅 嘫.17
傑偨丄AF偑EG偵懳偡傞傛偆偵AI偑EK偵懳偟丄EG偑FG偵懳偡傞傛偆偵EK偑FK偵懳偡傞丅 嘫.1
傛偭偰丄EK偼AI,FK偺斾椺拞崁偱偁傞丅 丂傑偨丄MN偼惓曽宍LM,NO偺斾椺拞崁偱偁傝丄AI偼LM丄FK偼NO偵摍偟偄丅 丂傛偭偰丄EK偼MN偵摍偟偄丅
傑偨丄DH偼EK,LO偼MN偵摍偟偄偺偱慡懱DK偼僌僲乕儌儞UVW偲NO偺榓偵摍偟偄丅
偙偺偲偒丄慡懱AK偼惓曽宍LM,NO偺榓偵摍偟偔丄DK偼僌僲乕儌儞UVW丄惓曽宍NO偵摍偟偄偺偱巆傝偺AB偼ST偡側傢偪LM偱偱偒偨惓曽宍偵摍偟偄丅傛偭偰丄LM偼柺愊AB偵摍偟偄惓曽宍偺曈偱偁傞丅
LN偑楎慄暘偲傛偽傟傞柍棟慄暘偱偁傞偙偲傪帵偡丅
AK偼桳棟柺愊偱LP,PN偱偱偒偨惓曽宍偺榓偵摍偟偄偺偱丄LP,PN偱偱偒偨惓曽宍偺榓偼桳棟柺愊偱偁傞丅
DK偼拞崁側偺偱丆DK偼挿曽宍LP,PN偺2攞偵摍偟偔丆備偊偵挿曽宍LP,PN傕拞崁偱偁傞丅
傑偨丄AI偼FK偲捠栺晄壜擻偱偁傞偙偲偑徹柧偝傟偰偄傞偺偱丄LP偱偱偒偨惓曽宍偼PN偱偱偒偨惓曽宍偲捠栺晄壜擻偱偁傞丅
傛偭偰丄LP,PN偼LP,PN偱偱偒偨惓曽宍偺榓傪桳棟柺愊丄挿曽宍LP,PN偺2攞傪拞崁柺愊偲偡傞暯曽偵偍偄偰捠栺晄壜擻側慄暘偱偁傞丅
備偊偵丄LM偼楎慄暘偲傛偽傟傞柍棟慄暘偱丄柺愊AB偵摍偟偄惓曽宍偺曈偱偁傞丅 嘳.76
偟偨偑偭偰丄柺愊AB偵摍偟偄惓曽宍偺曈偼楎慄暘偱偁傞丅
徹柧廔椆