柦戣101
乽拞崁柺愊偲桳棟柺愊偺嵎偵摍偟偄惓曽宍偺曈忋偺惓曽宍偵摍偟偄挿曽宍偑桳棟慄暘忋偵嶌傜傟傞側傜偽丆戞5偺梋慄暘傪暆偲偡傞乿

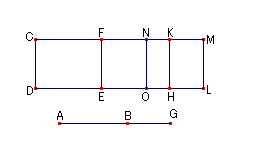
拞崁柺愊偲桳棟柺愊偺嵎偵摍偟偄惓曽宍偺曈傪AB偲偟丆CD偼桳棟慄暘偱偁傞偲偟丆AB忋偺惓曽宍偵摍偟偔CF傪暆偲偡傞CE偑CD忋偵嶌傜傟傞偲偡傞丅
CF偑戞5偺梋慄暘偱偁傞偙偲傪帵偡丅
偦偟偰偦傟偼桳棟慄暘CD忋偵嶌傜傟CM傪暆偲偡傞偺偱丆備偊偵CM偼桳棟偱CD偲捠栺晄壜擻偱偁傞丅 嘳.22
慡懱偺CL偼AG忋丆GB忋偺惓曽宍偺榓偵摍偟偔丆偙傟傛傝CE偼AB忋偺惓曽宍偵摍偟偔丆備偊偵巆傝偺FL偼挿曽宍AG,GB偺2攞偵摍偟偄丅 嘦.7
FM偼N偱2摍暘偝傟丆N傪捠傝CD偐ML偺偳偪傜偐偵暯峴側捈慄NO偑堷偐傟偨偲偡傞丅偦偺偲偒丆挿曽宍FO偲NL偼偲傕偵挿曽宍AG,GB偵摍偟偄丅
傑偨丆挿曽宍AG,GB偺俀攞偼桳棟偱FL偵摍偟偔丆備偊偵FL偼桳棟偱偁傞丅
偦偟偰偦傟偼桳棟慄暘EF忋偵嶌傜傟FM傪暆偲偡傞偺偱丆備偊偵FM偼桳棟偱CD偲挿偝偵偍偄偰捠栺壜擻偱偁傞丅 嘳.20
偝偰丆CL偼拞崁偱丆FL偼桳棟偱丆備偊偵CL偼FL偲捠栺晄壜擻偱偁傞丅
傑偨丆CL偑FL偵懳偡傞傛偆偵CM偼MF偵懳偟丆備偊偵CM偼MF偲挿偝偵偍偄偰捠栺晄壜擻偱偁傞丅 嘫.1 嘳.11
傑偨丆椉曽偲傕桳棟偱丆備偊偵CM偲MF偼暯曽偵偍偄偰偺傒捠栺壜擻側桳棟慄暘偱偁傞丅備偊偵丆CF偼梋慄暘偱偁傞丅 嘳.73
師偵戞5偺梋慄暘偱偁傞偙偲傪帵偡丅
摨條偵偟偰丆挿曽宍CK,KM偑GB忋偺惓曽宍丆偡側傢偪FM忋偺惓曽宍偺4暘偺1偵摍偟偄丅
傑偨丆AG忋偺惓曽宍偼GB忋偺惓曽宍偲捠栺晄壜擻偱丆AG忋偺惓曽宍偼CH偵摍偟偔丆GB忋偺惓曽宍偼KL偵摍偟偄偺偱丆備偊偵CH偼KL偲捠栺晄壜擻偱偁傞丅
CH偑KL偵懳偡傞傛偆偵CK偼KM偵懳偟丆備偊偵CK偼KM偲挿偝偵偍偄偰捠栺晄壜擻偱偁傞丅 嘫.1 嘳.11
CM偲MF偼俀偮偺摍偟偔側偄慄暘側偺偱丆FM忋偺惓曽宍偺4暘偺1偵摍偟偔惓曽宍偩偗寚偗偰偄傞暯峴巐曈宍偑CM忋偵嶌傜傟丆捠栺晄壜擻側2偮偺晹暘偵暘偗傞丅備偊偵丆CM忋偺惓曽宍偼MF忋偺惓曽宍傛傝CM偲捠栺晄壜擻側偣傫暘忋偺惓曽宍偩偗戝偒偄丅 嘳.18
傑偨丆偨偝傟偨FM偼掕傔傜傟偨桳棟慄暘CD偲捠栺壜擻偱丆備偊偵CF偼戞5偺梋慄暘偱偁傞丅 嘳.Def.嘨.5
偟偨偑偭偰丆拞崁柺愊偲桳棟柺愊偺嵎偵摍偟偄惓曽宍偺曈忋偺惓曽宍偵摍偟偄挿曽宍偑桳棟慄暘忋偵嶌傜傟傞側傜偽丆戞5偺梋慄暘傪暆偲偡傞
徹柧廔椆