命題110
「中項面積から全体と通約できない中項面積が引かれるならば,残りの2つの無理線分,すなわち第2の中項余線分か,2つの中項面積の差に等しい正方形の辺ができる」

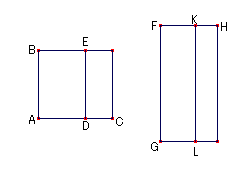
前と同じ図形を作図すると,中項面積BCから全体と通約不可能な面積BDが引かれるとする。
ECに等しい正方形に辺は2つの無理線分の1つ,すなわち第2の中項余線分か,2つの中項面積の差に等しい正方形の辺である事を証明する。
長方形BCとBDは中項で,BCはBDと通約不可能なので,ゆえに直線FHとFKは有理でFGと長さにおいて通約不可能である。 Ⅹ.22
BCはBDと,すなわちGHはGKと通約不可能なので,ゆえにHFもまたFKと通約不可能である。 Ⅵ.1 Ⅹ.11
ゆえに,FHとFKは平方においてのみ通約可能なゆり線分である。ゆえに,KHは余線分である。 Ⅹ.73
もし,FH上の正方形がFK上の正方形よりFHと通約可能な線分上の正方形だけ大きいならば,FHとFKの両方ともが定められた有理線分FGと長さにおいて通約可能であり,そのときKHは第3の余線分である。 Ⅹ.Def.Ⅲ.3
ところが,KLは有理で,有理線分と第3の余線分によって囲まれる長方形は無理なので,それに等しい正方形の辺は無理線分で,それを第2の中項余線分と呼ぶ。だから,LHに等しい正方形の辺,すなわちECに等しい正方形の辺は第2の中項余線分である。 Ⅹ.93
ところが,もしFH上の正方形がFK上の正方形よりFHと通約不可能菜線分上の正方形だけい大きいならば,直線HFとFKの両方ともがFGと長さにおいて通約可能であり,その時KHは第6の余線分である。 Ⅹ.Def.Ⅲ.6 Ⅹ.95
有理線分と第6の余線分によって囲まれる長方形に等しい正方形の辺は,2つの中項面積の差に等しい正方形の辺である。 Ⅹ.96
ゆえに,LHすなわちECに等しい正方形の辺は2つの中項面積の差に等しい正方形の辺である。
したがって,中項面積から全体と通約できない中項面積が引かれるならば,残りの2つの無理線分,すなわち第2の中項余線分か,2つの中項面積の差に等しい正方形の辺ができる。
証明終了