Lemma
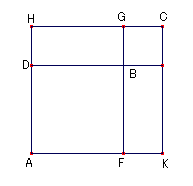
擇偮偺惓曽宍AB,BC偑偁傝丆DB偑BE偲摨堦捈慄忋偵偁傞傛偆偵偡傞丅
偦偺偲偒FB傕BG偲摨堦捈慄忋偵偁傞丅偦偟偰暯峴巐曈宍AC偑姰惉偝傟偨偲偡傞丅

偙偙偱丆AC偼惓曽宍偱偁傝丆DB偼AB,BC偺 斾椺拞崁偝傜偵DC偼AC,CB偺斾椺拞崁偱偁傞偙偲傪帵偡丅
DB偼BF偲摍偟偄偺偱丆BE偲BG傕摍偟偄丅 傛偭偰丆慡懱偺DE偲慡懱偺FG傕摍偟偄丅
偙偙偱DE偼捈慄AH丆KC偺偦傟偧傟偲摍偟偄丅偦偟偰FG偼捈慄AK偲HC偲摍偟偄丅
傛偭偰丆AH,KC偼AK,HC偲摍偟偄丅
嘥.34
傛偭偰丆暯峴巐曈宍AC偼摍曈宍偱偁傞丅偦偟偰挿曽宍偱傕偁傞丅
傛偭偰AC偼惓曽宍偱偁傞丅
FB偑BG偵懳偡傞傛偆偵DB傕BE偵懳偡傞丅
堦曽FB偑BG偵懳偡傞傛偆偵AB偑DG偵懳偡傞丅
偦偟偰DB偑BE偵懳偡傞傛偆偵DG偑BC偵懳偡傞丅
傛偭偰AB偑DG偵懳偡傞傛偆偵丆DG偑BC偵懳偡傞丅
嘫.1
嘫.11
傛偭偰丆DG偼AB偲BC偺斾椺拞崁偱偁傞丅
偮偓偵丆DC傕AC偲CB偺斾椺拞崁偱偁傞偙偲傪帵偡丅
AD偑DK偵懳偡傞傛偆偵KG偼GC偵懳偟丆偦傟偧傟偼摍偟偄偺偱 偁傢偣偨AK偵懳偡傞KD偼KC偑CG偵懳偡傞偺偲摍偟偄丅 嘪.18
堦曽AK偑KD偵懳偡傞傛偆偵AC偑CD偵懳偡傞丅
偦偟偰KC偑CG偵懳偡傞傛偆偵DC偑CB偵懳偡傞丅
傛偭偰AC偑DC偵懳偡傞傛偆偵DC偑BC偵懳偡傞丅
嘫.1
嘫.11
傛偭偰丆DC偼AC丆CB偺斾椺拞崁偱偁傞丅
柦戣54
桳棟慄暘偲戞堦偺擇崁慄暘偱嶌傜傟傞柺愊側傜偽丆
偦偺帪丆偦偺柺愊偲摍偟偄
惓曽宍偺堦曈偼柍棟慄暘偱擇崁慄暘偲傛偽傟傞丅
柺愊AC偼桳棟慄暘AB偲戞堦偺擇崁慄暘AD偱偮偔傜傟偰偄傞偲偡傞丅
AC偲摨偠柺愊偺惓曽宍偺堦曈偑擇崁慄暘偲 屇偽傟傞柍棟慄暘偱偁傞偙偲傪帵偡丅
AD偼戞堦偺擇崁慄暘偱偁傞偺偱丆E偱暘妱偝傟傞丅 偦偟偰AE偺傎偆偑戝偒偄偲偡傞丅
偦偺偲偒AE偲ED偼暯曽偵偍偄偰偺傒
捠栺壜擻偱AE偺惓曽宍偼ED偺惓曽宍傛傝
AE偲捠栺壜擻側捈慄忋偺惓曽宍偩偗戝偒偔丅
AE偼桳棟慄暘AB偲挿偝偵偍偄偰捠栺壜擻偱偁傞偙偲偼柧傜偐偱偁傞丅
嘳.Def,嘦.1
ED傪F偱偵摍暘偡傞丅
偙偺偲偒丆AE偺惓曽宍偼ED偺惓曽宍傛傝 AE偲捠栺壜擻側捈慄忋偺惓曽宍偩偗戝偒偄丅
傛偭偰丆傕偟戝偒偄傎偆AE忋偵丆彫偝偄傎偆偺慄暘忋偺惓曽宍偺巐暘偺堦丆 偮傑傝EF忋偺惓曽宍偵摍偟偔惓曽宍偩偗寚偗偰偄傞暯峴巐曈宍偑 偁傞側傜偽丆 偦偺帪偦傟傪捠栺壜擻側晹暘偵暘偗傞丅 嘳.17
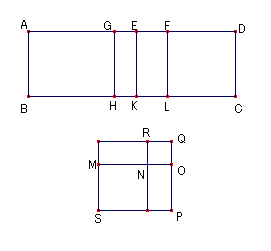
AE忋偵EF忋偺惓曽宍偲摍偟偄挿曽宍AG丆GE偑偁傞偲偡傞丅
偦偺偲偒AG偼EG偲挿偝偵偍偄偰捠栺壜擻偱偁傞丅
G,E,F偐傜偦傟偧傟捈慄AB丆CD偲暯峴側GH,EK,FL傪昤偔丅
暯峴巐曈宍AH偵摍偟偄惓曽宍SN偑嶌傜傟丆 GK偵摍偟偄惓曽宍NQ偑嶌傜傟偨偲偡傞丅
MN偑NO偲摨堦捈慄忋偵側傞傛偆偵偟丆
傑偨RN傕NP偲摨堦捈慄忋偵側傞傛偆偵偡傞丅
偦偟偰暯峴巐曈宍SQ偑姰惉偟丆SQ偼惓曽宍偱偁傞丅
嘦.4
偙偙偱挿曽宍AG丆GE偼惓曽宍EF偲摍偟偄偺偱丆 AG偑EF偵懳偡傞傛偆偵FE偑EG偵懳偡傞丅 嘫.17
傛偭偰丆AH偑EL偵懳偡傞傛偆偵EL偑KG偵懳偡傞丅
傛偭偰丆EL偼AH偲GK偺斾椺拞崁偱偁傞丅
嘫.1
偙偙偱丆AH偲SN偼摍偟偔GK偲NQ傕摍偟偄偺偱丆
EL偼SN偲NG偺斾椺拞崁偱偁傞丅
偟偐偟丆MR傕摨偠SN偲NQ偺斾椺拞崁偱偁傞丅
傛偭偰EL偲MR偼摍偟偔,偮傑傝PO偵傕摍偟偄丅
偙偙偱丆AH偲GK傕SN偲NG偵摍偟偄丅
傛偭偰慡懱偺AC偼慡懱偺SQ偲摍偟偄丅偮傑傝,偦傟偼MO忋偺惓曽宍偲摍偟偔
MO偼AC偲摨偠柺愊偺惓曽宍偺堦曈偲側傞丅
師偵MO偑擇崁慄暘偱偁傞偙偲傪帵偡丅
AG偼GE偲捠栺壜擻偱偁傞偺偱 AE傕AG,GE偺偦傟偧傟偲捠栺壜擻偱偁傞丅 嘳.15
偙偙偱丆AE傕壖掕傛傝AB偲捠栺壜擻傛偭偰丆
AG偲GE傕AB偲捠栺壜擻偱偁傞丅
偦偟偰AB偼桳棟,傛偭偰丆AG,GE傕桳棟偱偁傞丅
嘳.12
傛偭偰,挿曽宍AH.GK傕桳棟偱AH偼GK偲捠栺壜擻偱偁傞丅 嘳.19
偟偐偟丆AH偼SN偲摍偟偔GK偼NQ偲摍偟偄,傛偭偰丆SN偲NQ偺榓 偮傑傝丆MN忋,NO忋偺惓曽宍偼桳棟偱,捠栺壜擻偱偁傞丅
AE偼ED偲挿偝偵偍偄偰捠栺晄壜擻丅堦曽AE偼AG偲捠栺壜擻丅
偦偟偰DE偼EF偲捠栺壜擻丅
傛偭偰AG傕EF偲捠栺晄壜擻偱AH傕EL偲捠栺晄壜擻偱偁傞丅
嘳.13
嘫.1
嘳.11
偟偐偟AH偼SN偲EL偼MR偲摍偟偄偺偱,SN傕MR偲捠栺晄壜擻丅
偟偐偟丆SN偑MR偵懳偡傞傛偆偵PN偑NR偵懳偡傞偺偱PN偼NR偲捠栺晄壜擻丅
偟偐偟PN偼MN偲NR偼NO偲摍偟偄丅傛偭偰丆MN偼NO偲捠栺晄壜擻丅
嘫.1
嘳.11
偦偟偰MN忋偺惓曽宍偼NO忋偺惓曽宍偲 捠栺壜擻偱,偦傟偧傟偑桳棟偱偁傞丅
傛偭偰丆MN偲NO偼暯曽偵偍偄偰偺傒捠栺壜擻側桳棟慄暘偱偁傞丅
傛偭偰丆MO偼AC偲摍偟偄惓曽宍偺堦曈偱偁傞擇崁慄暘偱偁傞丅 嘳.36
徹柧廔椆